8. (2010湖北文)17.(本小题满分12分)

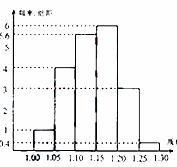　 为了了解一个小水库中养殖的鱼有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量(单位：千克)，并将所得数据分组，画出频率分布直方图(如图所示)

(Ⅰ)在答题卡上的表格中填写相应的频率；

(Ⅱ)估计数据落在(1.15,1.30)中的概率为多少；

(Ⅲ)将上面捕捞的100条鱼分别作一记号后再放回水库，几天后再从水库的多处不同位置捕捞出120条鱼，其中带有记号的鱼有6条，请根据这一情况来估计该水库中鱼的总条数。

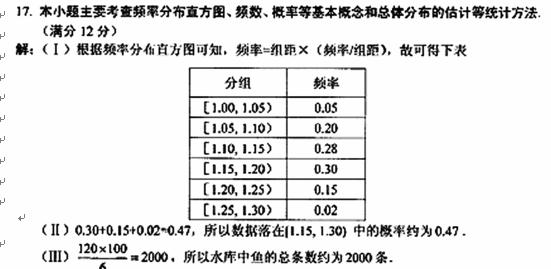
7. (2010广东理)17.(本小题满分12分)

某食品厂为了检查一条自动包装流水线的生产情况，随即抽取该流水线上40件产品作为样本算出他们的重量(单位：克)重量的分组区间为(490,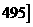，(495,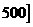，……(510,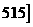，由此得到样本的频率分布直方图，如图4所示．

　 (1)根据频率分布直方图，求重量超过505克的产品数量．

　 (2)在上述抽取的40件产品中任取2件，设Y为重量超过505克的产品数量，求Y的分布列．

　 (3)从流水线上任取5件产品，求恰有2件产品合格的重量超过505克的概率．

6. (2010天津文)(18)(本小题满分12分)

有编号为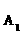,,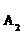…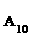的10个零件，测量其直径(单位：cm)，得到下面数据：

其中直径在区间[1.48，1.52]内的零件为一等品。

(Ⅰ)从上述10个零件中，随机抽取一个，求这个零件为一等品的概率；

(Ⅱ)从一等品零件中，随机抽取2个.

　　 (ⅰ)用零件的编号列出所有可能的抽取结果；

　　 (ⅱ)求这2个零件直径相等的概率。本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识，考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分

　[解析](Ⅰ)解：由所给数据可知，一等品零件共有6个.设“从10个零件中，随机抽取一个为一等品”为事件A，则P(A)==.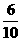

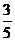　　　 (Ⅱ)(i)解：一等品零件的编号为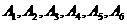.从这6个一等品零件中随机抽取2个，所有可能的结果有：,,,

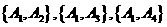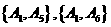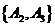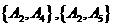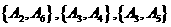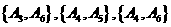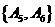,,,共有15种.

　　　 (ii)解：“从一等品零件中，随机抽取的2个零件直径相等”(记为事件B)的所有可能结果有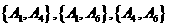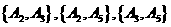：，，共有6种.

　　　 所以P(B)=.

5. (2010安徽文)18、(本小题满分13分)

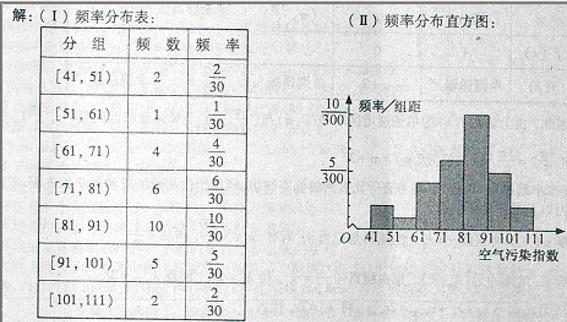
　 某市2010年4月1日-4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):

　　　　 61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,

　　　　 77,86,81,83,82,82,64,79,86,85,75,71,49,45,

(Ⅰ)　 完成频率分布表；

(Ⅱ)作出频率分布直方图；

(Ⅲ)根据国家标准，污染指数在0~50之间时，空气质量为优：在51~100之间时，为良；在101~150之间时，为轻微污染；在151~200之间时，为轻度污染。

请你依据所给数据和上述标准，对该市的空气质量给出一个简短评价.

[命题意图]本题考查频数，频率及频率分布直方图，考查运用统计知识解决简单实际问题的能力，数据处理能力和运用意识.

[解题指导](1)首先根据题目中的数据完成频率分布表，作出频率分布直方图，根据污染指数，确定空气质量为优、良、轻微污染、轻度污染的天数。

(Ⅲ)答对下述两条中的一条即可：

(1)　　 该市一个月中空气污染指数有2天处于优的水平，占当月天数的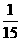，有26天处于良的水平，占当月天数的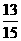，处于优或良的天数共有28天，占当月天数的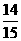。说明该市空气质量基本良好。

(2)　　 轻微污染有2天，占当月天数的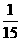。污染指数在80以上的接近轻微污染的天数有15天，加上处于轻微污染的天数，共有17天，占当月天数的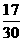，超过50%，说明该市空气质量有待进一步改善。

[规律总结]在频率分布表中，频数的和等于样本容量，频率的和等于1，每一小组的频率等于这一组的频数除以样本容量.频率分布直方图中，小矩形的高等于每一组的频率/组距，它们与频数成正比，小矩形的面积等于这一组的频率.对于开放性问题的回答，要选择适当的数据特征进行考察，根据数据特征分析得出实际问题的结论.

4.(2010辽宁理)(18)(本小题满分12分)

　　 为了比较注射A, B两种药物后产生的皮肤疱疹的面积，选200只家兔做试验，将这200只家兔随机地分成两组，每组100只，其中一组注射药物A，另一组注射药物B。

　　 (Ⅰ)甲、乙是200只家兔中的2只，求甲、乙分在不同组的概率；

(Ⅱ)下表1和表2分别是注射药物A和B后的试验结果.(疱疹面积单位：mm²)

表1：注射药物A后皮肤疱疹面积的频数分布表

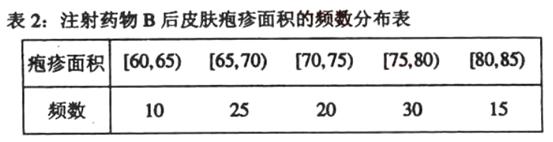
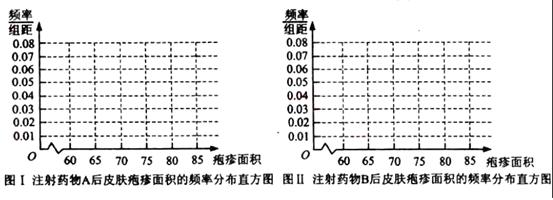
(ⅰ)完成下面频率分布直方图，并比较注射两种药物后疱疹面积的中位数大小；

(ⅱ)完成下面2×2列联表，并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”.

表3：

解：

(Ⅰ)甲、乙两只家兔分在不同组的概率为

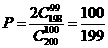　　　 　　　　　　　　　　　　　　　　　　……4分

(Ⅱ)(i)

图Ⅰ注射药物A后皮肤疱疹面积的频率分布直方图　　 图Ⅱ注射药物B后皮肤疱疹面积的频率分布直方图

可以看出注射药物A后的疱疹面积的中位数在65至70之间，而注射药物B后的疱疹面积的中位数在70至75之间，所以注射药物A后疱疹面积的中位数小于注射药物B后疱疹面积的中位数。　　　　　　　　　　　　　　　　　　　　 ……8分

(ii)表3：

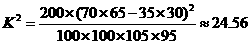
由于K²＞10.828，所以有99.9%的把握认为“注射药物A后的疱疹面积于注射药物B后的疱疹面积有差异”。　　　　　　　　　　　　　　　　　　　 ……12分

3.(2010辽宁文)(18)(本小题满分12分)

为了比较注射A,B两种药物后产生的皮肤疱疹的面积，选200只家兔做实验，将这200只家兔随机地分成两组。每组100只，其中一组注射药物A，另一组注射药物B。下表1和表2分别是注射药物A和药物B后的实验结果。(疱疹面积单位：)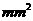

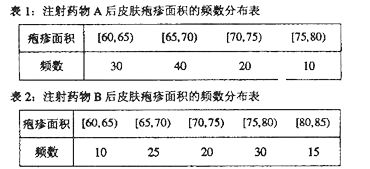
(Ⅰ)完成下面频率分布直方图，并比较注射两种药物后疱疹面积的中位数大小；

(Ⅱ)完成下面列联表，并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”。

附：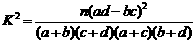

解：

　 (Ⅰ)

图1注射药物A后皮肤疱疹面积的频率分布直方图　　 图2注射药物B后皮肤疱疹面积的频率分布直方图

　　 可以看出注射药物A后的疱疹面积的中位数在65至70之间，而注射药物B后的疱疹面积的中位数在70至75之间，所以注射药物A后疱疹面积的中位数小于注射药物B后疱疹面积的中位数。

　 (Ⅱ)表3

	疱疹面积小于	疱疹面积不小于	合计
注射药物
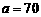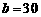注射药物
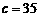合计

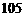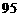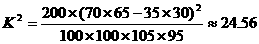
　　 由于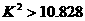，所以有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”.

2.(2010陕西文)19 (本小题满分12分)

为了解学生身高情况，某校以10%的比例对全校700名学生按性别进行出样检查，测得身高情况的统计图如下：

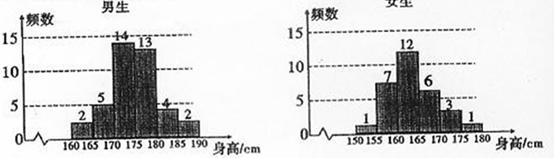
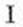()估计该校男生的人数；

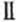()估计该校学生身高在170~185cm之间的概率；

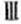()从样本中身高在180~190cm之间的男生中任选2人，求至少有1人身高在185~190cm之间的概率。

解 (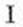)样本中男生人数为40 ，由分层出样比例为10%估计全校男生人数为400。

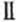()有统计图知，样本中身高在170~185cm之间的学生有14+13+4+3+1=35人，样本容量为70 ，所以样本中学生身高在170~185cm之间的频率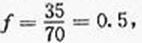故有f估计该校学生身高在170~180cm之间的概率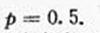

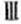()样本中身高在180~185cm之间的男生有4人，设其编号为

　　　 样本中身高在185~190cm之间的男生有2人，设其编号为

从上述6人中任取2人的树状图为：

故从样本中身高在180~190cm之间的男生中任选2人得所有可能结果数为15，求至少有1人身高在185~190cm之间的可能结果数为9，因此，所求概率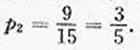

1.(2010湖南文)17. (本小题满分12分)

为了对某课题进行研究，用分层抽样方法从三所高校A,B,C的相关人员中，抽取若干人组成研究小组、有关数据见下表(单位：人)

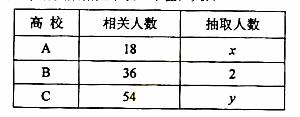
(I)　　　　　　　　　 求x,y ;

(II)　　　　　　　 若从高校B、C抽取的人中选2人作专题发言，求这二人都来自高校C的概率。

4.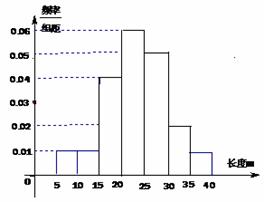(2010江苏卷)4、某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标)，所得数据都在区间[5,40]中，其频率分布直方图如图所示，则其抽样的100根中，有____根在棉花纤维的长度小于20mm。

[解析]考查频率分布直方图的知识。

100×(0.001+0.001+0.004)×5=30

3.(2010福建文)14． 将容量为n的样本中的数据分成6组，绘制频率分布直方图。若第一组至第六组数据的频率之比为2：3：4：6：4：1，且前三组数据的频数之和等于27，则n等于　　　　　 。

[答案]60

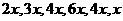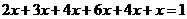[解析]设第一组至第六组数据的频率分别为，则，解得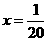，所以前三组数据的频率分别是，

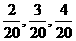故前三组数据的频数之和等于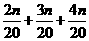=27，解得n=60。

[命题意图]本小题考查频率分布直方图的基础知识，熟练基本公式是解答好本题的关键。