8.(2009年广东卷文)某单位200名职工的年龄分布情况如图2，现要从中抽取40名职工作样本，用系统抽样法，将全体职工随机按1－200编号，并按编号顺序平均分为40组(1－5号，6－10号…，196－200号).若第5组抽出的号码为22，则第8组抽出的号码应是　　 。若用分层抽样方法，则40岁以下年龄段应抽取　　　 人.

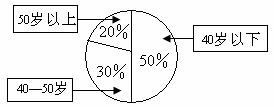
　　　　　　　　 　　　　　　　　　　　图 2

答案　 37,　 20

解析　 由分组可知,抽号的间隔为5,又因为第5组抽出的号码为22，所以第6组抽出的号

码为27，第7组抽出的号码为32，第8组抽出的号码为37.

　 40岁以下年龄段的职工数为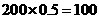,则应抽取的人数为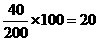人.

7.(2009上海卷理)在发生某公共卫生事件期间，有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天，每天新增疑似病例不超过7人”。根据过去10天甲、乙、丙、丁四地新增疑似病例数据，一定符合该标志的是

A.甲地：总体均值为3，中位数为4　　 B.乙地：总体均值为1，总体方差大于0　　　

C.丙地：中位数为2，众数为3　　　　 D.丁地：总体均值为2，总体方差为3

答案　 D 　　　　　　

解析　 根据信息可知，连续10天内，每天的新增疑似病例不能有超过7的数，选项A中，中位数为4，可能存在大于7的数；同理，在选项C中也有可能；选项B中的总体方差大于0，叙述不明确，如果数目太大，也有可能存在大于7的数；选项D中，根据方差公式，如果有大于7的数存在，那么方差不会为3，故答案选D.

6.(2009福建卷文)一个容量100的样本，其数据的分组与各组的频数如下表

组别
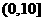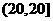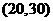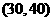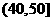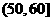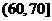频数	12	13	24	15	16	13	7

则样本数据落在上的频率为

A. 0.13　　　　　　 B. 0.39　 　　　　　C. 0.52　　　　　 D. 0.64

答案　 C

解析　 由题意可知频数在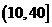的有：13+24+15=52，由频率=频数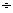总数可得0.52.

5.(2009陕西卷文)某单位共有老、中、青职工430人,其中青年职工160人，中年职工人数是老年职工人数的2倍。为了解职工身体状况，现采用分层抽样方法进行调查，在抽取的样本中有青年职工32人，则该样本中的老年职工人数为

A.9　 　　　　 　　　　　 B.18 　　　　　　　　　 C.27　　　　　　　　　　 　　D. 36

答案　 B　

　解析　 由比例可得该单位老年职工共有90人，用分层抽样的比例应抽取18人.

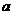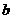4.(2009四川卷文)设矩形的长为，宽为，其比满足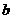∶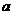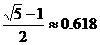＝，这种矩形给人以美感，称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本：

甲批次：0.598　 0.625　 0.628　 0.595　 0.639

乙批次：0.618　 0.613　 0.592　 0.622　 0.620

根据上述两个样本来估计两个批次的总体平均数，与标准值0.618比较，正确结论是

　 A.甲批次的总体平均数与标准值更接近

　 B.乙批次的总体平均数与标准值更接近

　 C.两个批次总体平均数与标准值接近程度相同

　 D.两个批次总体平均数与标准值接近程度不能确定

答案　 A

解析 甲批次的平均数为0.617，乙批次的平均数为0.613

备考提示　 用以上各数据与0.618(或0.6)的差进行计算，以减少计算量，说明多思则少算。

3.(2009宁夏海南卷理)对变量x, y 有观测数据理力争(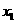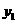，)(i=1,2,…，10)，得散点图1；对变量u ，v 有观测数据(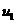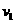，)(i=1,2,…，10),得散点图2. 由这两个散点图可以判断。

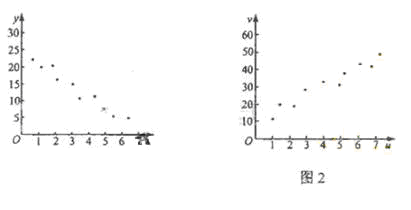
A.变量x 与y 正相关，u 与v 正相关　　 B.变量x 与y 正相关，u 与v 负相关

C.变量x 与y 负相关，u 与v 正相关　　 D.变量x 与y 负相关，u 与v 负相关

答案　 C

解析　 由这两个散点图可以判断,变量x 与y 负相关，u 与v 正相关,选C.

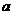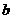2.(2009四川卷文)设矩形的长为，宽为，其比满足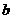∶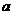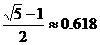＝，这种矩形给人以美感，称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本：

甲批次：0.598　 0.625　 0.628　 0.595　 0.639

乙批次：0.618　 0.613　 0.592　 0.622　 0.620

根据上述两个样本来估计两个批次的总体平均数，与标准值0.618比较，正确结论是

　 A.甲批次的总体平均数与标准值更接近

　 B.乙批次的总体平均数与标准值更接近

　 C.两个批次总体平均数与标准值接近程度相同

　 D.两个批次总体平均数与标准值接近程度不能确定

答案　 A

解析　 甲批次的平均数为0.617，乙批次的平均数为0.613

1.(2009山东卷理)某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的 　　

产品净重(单位：克)数据绘制的频率分布直方图，其中产品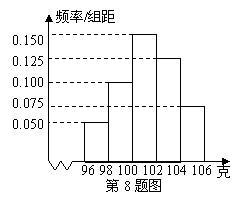

净重的范围是[96，106]，样本数据分组为[96，98)，[98，100),

[100，102)，[102，104),[104，106],已知样本中产品净重小于

100克的个数是36，则样本中净重大于或等于98克并且

小于104克的产品的个数是　　　　　　　　　 (　　　 ).

A.90　　 　　　B.75　　　　　 C.　 60　　　　　 D.45

答案 A

解析　 产品净重小于100克的概率为(0.050+0.100)×2=0.300,

已知样本中产品净重小于100克的个数是36,设样本容量为,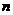

则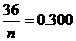,所以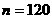,净重大于或等于98克并且小于

104克的产品的概率为(0.100+0.150+0.125)×2=0.75,所以样本

中净重大于或等于98克并且小于104克的产品的个数是

120×0.75=90.故选A.

[命题立意]:本题考查了统计与概率的知识,读懂频率分布直方图,会计算概率以及样本中有关的数据.

10. (2010安徽理)21、(本小题满分13分)

　　 品酒师需定期接受酒味鉴别功能测试，一种通常采用的测试方法如下：拿出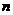瓶外观相同但品质不同的酒让其品尝，要求其按品质优劣为它们排序；经过一段时间，等其记忆淡忘之后，再让其品尝这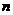瓶酒，并重新按品质优劣为它们排序，这称为一轮测试。根据一轮测试中的两次排序的偏离程度的高低为其评为。

　　 现设，分别以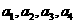表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号，并令

，

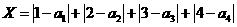则是对两次排序的偏离程度的一种描述。

　　 (Ⅰ)写出的可能值集合；

(Ⅱ)假设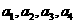等可能地为1,2,3,4的各种排列，求的分布列；

(Ⅲ)某品酒师在相继进行的三轮测试中，都有，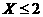

(i)试按(Ⅱ)中的结果，计算出现这种现象的概率(假定各轮测试相互独立)；

(ii)你认为该品酒师的酒味鉴别功能如何？说明理由。

2009年高考题

9. (2010湖南理)17．(本小题满分12分)

图4是某城市通过抽样得到的居民某年的月均用水量(单位：吨)的频率分布直方图

(Ⅰ)求直方图中x的值

(II)若将频率视为概率，从这个城市随机抽取3位居民(看作有放回的抽样)，求月均用水量在3至4吨的居民数X的分布列和数学期望。