4．乙品种棉花的纤维长度基本上是对称的，而且大多集中在中间(均值附近)．甲品种

棉花的纤维长度除一个特殊值(352)外，也大致对称，其分布较均匀．

3．甲品种棉花的纤维长度的中位数为307mm，乙品种棉花的纤维长度的中位数为318mm．

2．甲品种棉花的纤维长度较乙品种棉花的纤维长度更分散．(或：乙品种棉花的纤维长

度较甲品种棉花的纤维长度更集中(稳定)．甲品种棉花的纤维长度的分散程度比乙品

种棉花的纤维长度的分散程度更大)．

8.(2008海南、宁夏)从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位：mm)，结果如下：

甲品种：271　273　280　285　285　 287　292　294　295　301　303　303　307

　　 　 　　308　310　314　319　323　325　325　 328　331　334　337　352

乙品种：284　292　295　304　306　307　312　313　315　315　316　318　318

　　　　 　 320　322　322　324　327　329　331　333　336　337　343　356

由以上数据设计了如下茎叶图

根据以上茎叶图，对甲、乙两品种棉花的纤维长度作比较，写出两个统计结论：

①　　　　　　　　；②　　　　　　　　．

解析　 1．乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度(或：乙品种棉花

的纤维长度普遍大于甲品种棉花的纤维长度)．

7.(2008广东)某初级中学共有学生2000名，各年级男、女生人数如下表：

已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19.

(1)求x的值；

(2)现用分层抽样的方法在全校抽取48名学生，问应在初三年级抽取多少名？

(3)已知y245,z245,求初三年级中女生比男生多的概率.

解　 (1)　 　　　　　　　

　　 (2)初三年级人数为y+z＝2000－373+377+380+370)＝500，

　　 现用分层抽样的方法在全校抽取48名学生，应在初三年级抽取的人数为：

　名

(3)设初三年级女生比男生多的事件为A ，初三年级女生男生数记为(y，z)；

　由(2)知 　，且　 ,基本事件空间包含的基本事件有：

(245，255)、(246，254)、(247，253)、……(255，245)共11个

事件A包含的基本事件有：　　　　　　　　　　　　　　

(251，249)、(252，248)、(253，247)、(254,246)、(255,245) 共5个

6.(2008广东理)某校共有学生2000名，各年级男、女生人数如下表．已知在全校 学生中随机抽取1名，抽到二年级女生的概率是0.19．现用分层抽样的方法在全校抽取64名学生，则应在三年级抽取的学生人数为　　　　　　　　　　　　　　　　 (　 )

	一年级	二年级	三年级
女生	373
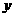男生	377	370

A．24　　 　 　　　　　　B．18　　 　 　C.16　 　 　　　　　 D.12　　

答案　 C

解析　 依题意我们知道二年级的女生有380人，那么三年级的学生的人数应该是，

即总体中各个年级的人数比例为，故在分层抽样中应在三年级抽取的学生人数为

5、(2008山东文)从某项综合能力测试中抽取100人的成绩，统计如表，则这100人成绩的标准差为(　　 )

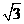A．　　　 　　　 B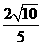．　　　　 　　 C．3　 　　　 D．

_{答案　 B}

解析　 本小题主要考查平均数、方差、标准差的概念及其运算.

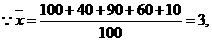
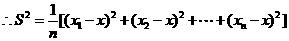
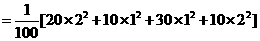
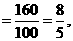
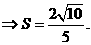
4.(2008湖南)对有n(n≥4)个元素的总体进行抽样，先将总体分成两个子总体和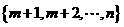 (m是给定的正整数，且2≤m≤n-2),再从每个子总体中各随机抽取2个元素组成样本.用表示元素i和j同时出现在样本中的概率，则=　　 ; 所有 (1≤i＜j≤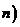的和等于　　 .

答案　 　　,6

3.(2008上海)已知总体的各个体的值由小到大依次为2,3,3,7,a,b,12，13.7，18.3，20，且总体的中位数为10.5，若要使该总体的方差最小，则a、b的取值分别是　　　

答案　 10.5和10.5

2.(2008天津)一个单位共有职工200人，其中不超过45岁的有120人，超过45岁的有

80人．为了调查职工的健康状况，用分层抽样的方法从全体职工中抽取一个容量为25的样本，应抽取超过45岁的职工________________人．

答案　 10