
题目列表(包括答案和解析)
4、(09安徽理12)以直角坐标系的原点为极点, 轴的正半轴为极轴,并在两种坐标系中
轴的正半轴为极轴,并在两种坐标系中
取相同的长度单位。已知直线的极坐标方程为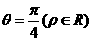 ,它与曲线
,它与曲线
(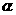 为参数)相交于两点A和B,则|AB|=_______.
为参数)相交于两点A和B,则|AB|=_______.
[解析]直线的普通方程为 ,曲线的普通方程
,曲线的普通方程
∴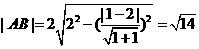
 答案
答案
3、(天津理13) 设直线 的参数方程为
的参数方程为 (t为参数),直线
(t为参数),直线 的方程为y=3x+4则
的方程为y=3x+4则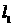 与
与 的距离为_______
的距离为_______
[解析]由题直线 的普通方程为
的普通方程为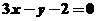 ,故它与与
,故它与与 的距离为
的距离为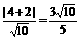 。
。
答案 
2、(09广东理15) (几何证明选讲选做题)如图3,点A、B、C是圆O上的点,且AB=4, ,则圆O的面积等于 .
,则圆O的面积等于 .

图3
[解析]连结AO,OB,因为  ,所以
,所以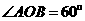 ,
, 为等边三角形,故圆
为等边三角形,故圆
O的半径 ,圆O的面积
,圆O的面积 .
.
答案

1、(09广东理14)(坐标系与参数方程选做题)若直线 (t为参数)与直线
(t为参数)与直线 垂直,则常数
垂直,则常数 = .
= .
[解析]将 化为普通方程为
化为普通方程为 ,斜率
,斜率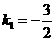 ,
,
当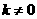 时,直线
时,直线 的斜率
的斜率 ,由
,由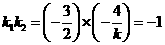 得
得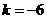 ;
;
当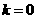 时,直线
时,直线 与直线
与直线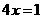 不垂直.
不垂直.
综上可知,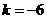 .
.
答案 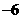
5.(2010江苏卷)21.[选做题]本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答。若多做,则按作答的前两题评分。解答时应写出文字说明、证明过程或演算步骤。
A.  选修4-1:几何证明选讲
选修4-1:几何证明选讲
(本小题满分10分)
AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB延长线于点C,若DA=DC,求证:AB=2BC。
[解析] 本题主要考查三角形、圆的有关知识,考查推理论证能力。
 (方法一)证明:连结OD,则:OD⊥DC,
(方法一)证明:连结OD,则:OD⊥DC,
又OA=OD,DA=DC,所以∠DAO=∠ODA=∠DCO,
∠DOC=∠DAO+∠ODA=2∠DCO,
所以∠DCO=300,∠DOC=600,
所以OC=2OD,即OB=BC=OD=OA,所以AB=2BC。
(方法二)证明:连结OD、BD。
 因为AB是圆O的直径,所以∠ADB=900,AB=2 OB。
因为AB是圆O的直径,所以∠ADB=900,AB=2 OB。
因为DC 是圆O的切线,所以∠CDO=900。
又因为DA=DC,所以∠DAC=∠DCA,
于是△ADB≌△CDO,从而AB=CO。
即2OB=OB+BC,得OB=BC。
故AB=2BC。
B. 选修4-2:矩阵与变换
(本小题满分10分)
在平面直角坐标系xOy中,已知点A(0,0),B(-2,0),C(-2,1)。设k为非零实数,矩阵M=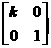 ,N=
,N= ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
[解析] 本题主要考查图形在矩阵对应的变换下的变化特点,考查运算求解能力。满分10分。
解:由题设得
由 ,可知A1(0,0)、B1(0,-2)、C1(
,可知A1(0,0)、B1(0,-2)、C1( ,-2)。
,-2)。
计算得△ABC面积的面积是1,△A1B1C1的面积是 ,则由题设知:
,则由题设知: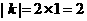 。
。
所以k的值为2或-2。
C. 选修4-4:坐标系与参数方程
(本小题满分10分)
在极坐标系中,已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值。
[解析] 本题主要考查曲线的极坐标方程等基本知识,考查转化问题的能力。满分10分。
解: ,圆ρ=2cosθ的普通方程为:
,圆ρ=2cosθ的普通方程为: ,
,
直线3ρcosθ+4ρsinθ+a=0的普通方程为: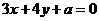 ,
,
又圆与直线相切,所以 解得:
解得: ,或
,或 。
。
D. 选修4-5:不等式选讲
(本小题满分10分)
设a、b是非负实数,求证: 。
。
[解析] 本题主要考查证明不等式的基本方法,考查推理论证的能力。满分10分。
(方法一)证明:
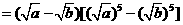

因为实数a、b≥0,
所以上式≥0。即有 。
。
(方法二)证明:由a、b是非负实数,作差得

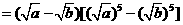
当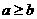 时,
时,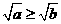 ,从而
,从而 ,得
,得 ;
;
当 时,
时, ,从而
,从而 ,得
,得 ;
;
所以 。
。
[必做题]第22题、第23题,每题10分,共计20分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
2009年高考题
4.(2010福建理)21.本题设有(1)(2)(3)三个选考题,每题7分,请考生任选2题做答,满分14分。如果多做,则按所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
(1)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵M= ,
, ,且
,且 ,
,
(Ⅰ)求实数 的值;(Ⅱ)求直线
的值;(Ⅱ)求直线 在矩阵M所对应的线性变换下的像的方程。
在矩阵M所对应的线性变换下的像的方程。
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在直角坐标系xoy中,直线 的参数方程为
的参数方程为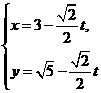 (t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 。
。
(Ⅰ)求圆C的直角坐标方程;(Ⅱ)设圆C与直线 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为 ,
,
求|PA|+|PB|。
(3)(本小题满分7分)选修4-5:不等式选讲
已知函数 。
。
(Ⅰ)若不等式 的解集为
的解集为 ,求实数
,求实数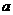 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若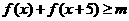 对一切实数x恒成立,求实数m的取值范围。
对一切实数x恒成立,求实数m的取值范围。
(1)选修4-2:矩阵与变换
[命题意图]本小题主要考查矩阵与变换等基础知识,考查运算求解能力。
[解析](Ⅰ)由题设得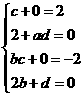 ,解得
,解得 ;
;
(Ⅱ)因为矩阵M所对应的线性变换将直线变成直线(或点),所以可取直线 上的两(0,0),(1,3),
上的两(0,0),(1,3),
由
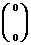 ,
,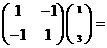
 得:点(0,0),(1,3)在矩阵M所对应的线性变换下的像是(0,0),(-2,2),从而
得:点(0,0),(1,3)在矩阵M所对应的线性变换下的像是(0,0),(-2,2),从而
直线 在矩阵M所对应的线性变换下的像的方程为
在矩阵M所对应的线性变换下的像的方程为 。
。
(2)选修4-4:坐标系与参数方程
[命题意图]本小题主要考查直线的参数方程、圆的极坐标方程、直线与圆的位置关系等基础知识,考查运算求解能力。
[解析](Ⅰ)由 得
得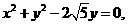 即
即
(Ⅱ)将 的参数方程代入圆C的直角坐标方程,得
的参数方程代入圆C的直角坐标方程,得 ,
,
即 由于
由于 ,故可设
,故可设 是上述方程的两实根,
是上述方程的两实根,
所以 故由上式及t的几何意义得:
故由上式及t的几何意义得:
|PA|+|PB|= =
=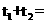
 。
。
(3)选修4-5:不等式选讲
[命题意图]本小题主要考查绝对值的意义、绝对值不等式等基础知识,考查运算求解能力。
[解析](Ⅰ)由 得
得 ,解得
,解得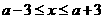 ,
,
又已知不等式 的解集为
的解集为 ,所以
,所以 ,解得
,解得 。
。
(Ⅱ)当 时,
时,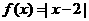 ,设
,设 ,于是
,于是
 =
= ,所以
,所以
当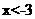 时,
时, ;当
;当 时,
时, ;当
;当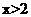 时,
时, 。
。
3.(2010辽宁理)(24)(本小题满分10分)选修4-5:不等式选讲
已知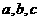 均为正数,证明:
均为正数,证明: ,并确定
,并确定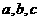 为何值时,等号成立。
为何值时,等号成立。
证明:(证法一)
因为a,b,c均为正数,由平均值不等式得
 ①
①
所以 ②
……6分
②
……6分
故 .
.
又 ③
③
所以原不等式成立. ……8分
当且仅当a=b=c时,①式和②式等号成立。当且仅当 时,③式等号成立。
时,③式等号成立。
即当且仅当a=b=c= 时,原式等号成立。
……10分
时,原式等号成立。
……10分
(证法二)
因为a,b,c均为正数,由基本不等式得
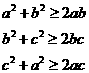
所以 ①
①
同理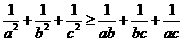 ②
……6分
②
……6分
故
 ③
③
所以原不等式成立. ……8分
当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c,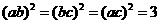 时,③式等号成立。
时,③式等号成立。
即当且仅当a=b=c= 时,原式等号成立。
……10分
时,原式等号成立。
……10分
2.(2010辽宁理)(23)(本小题满分10分)选修4-4:坐标系与参数方程

已知P为半圆C:
( 为参数,
为参数, )上的点,点A的坐标为(1,0),
)上的点,点A的坐标为(1,0),
O为坐标原点,点M在射线OP上,线段OM与C的弧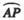 的长度均为
的长度均为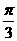 。
。
(I)以O为极点, 轴的正半轴为极轴建立极坐标系,求点M的极坐标;
轴的正半轴为极轴建立极坐标系,求点M的极坐标;
(II)求直线AM的参数方程。
解:
(Ⅰ)由已知,M点的极角为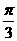 ,且M点的极径等于
,且M点的极径等于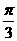 ,
,
故点M的极坐标为(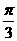 ,
,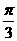 ).
……5分
).
……5分
(Ⅱ)M点的直角坐标为(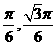 ),A(0,1),故直线AM的参数方程为
),A(0,1),故直线AM的参数方程为
 (t为参数)
……10分
(t为参数)
……10分
1.(2010辽宁理)(22)(本小题满分10分)选修4-1:几何证明选讲
 如图,
如图, 的角平分线AD的延长线交它的外接圆于点E
的角平分线AD的延长线交它的外接圆于点E
(I)证明:


(II)若 的面积
的面积 ,求
,求 的大小。
的大小。
证明:
(Ⅰ)由已知条件,可得
因为 是同弧上的圆周角,所以
是同弧上的圆周角,所以
故△ABE∽△ADC. ……5分
(Ⅱ)因为△ABE∽△ADC,所以 ,即AB·AC=AD·AE.
,即AB·AC=AD·AE.
又S=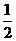 AB·ACsin
AB·ACsin ,且S=
,且S=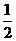 AD·AE,故AB·ACsin
AD·AE,故AB·ACsin =
AD·AE.
=
AD·AE.
则sin =1,又
=1,又 为三角形内角,所以
为三角形内角,所以 =90°.
……10分
=90°.
……10分
10. (2010广东文)14.(几何证明选讲选做题)如图3,在直角梯形ABCD中,DC∥AB,CB
(2010广东文)14.(几何证明选讲选做题)如图3,在直角梯形ABCD中,DC∥AB,CB ,AB=AD=
,AB=AD=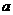 ,CD=
,CD= ,
,
点E,F分别为线段AB,AD的中点,则EF=
[答案]
解:连结DE,可知 为直角三角形。则EF是
为直角三角形。则EF是 斜边上的中线,等于斜边的一半,为
斜边上的中线,等于斜边的一半,为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com