
题目列表(包括答案和解析)
3.(2008广东理)(几何证明选讲选做题)已知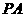 是圆
是圆 的切线,切点为
的切线,切点为 ,
, .
.
是圆 的直径,
的直径, 与圆
与圆 交于点
交于点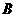 ,
,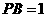 ,则圆
,则圆 的半径
的半径 .
.
答案 
2.(2008广东理)(不等式选讲选做题)已知 ,若关于
,若关于 的方程
的方程
有实根,则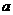 的取值范围是
.
的取值范围是
.
答案 
1.(2008广东理)(坐标系与参数方程选做题)已知曲线 的极坐标方
的极坐标方
程分别为 ,
, ,
,
则曲线 与
与 交点的极坐标为
.
交点的极坐标为
.
答案 
11、(09辽宁理24)(本小题满分10分)选修4-5:不等式选讲
设函数 。
。
(1)若 解不等式
解不等式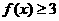 ;
;
(2)如果 ,
, ,求
,求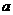 的取值范围。
的取值范围。
解(Ⅰ)当a=-1时,f(x)=︱x-1︳+︱x+1︳.
由f(x)≥3得
︱x-1︳+︱x+1|≥3
(ⅰ)x≤-1时,不等式化为
1-x-1-x≥3 即-2x≥3

2008年高考题
10、(09辽宁理23)(本小题满分10分)选修4-4 :坐标系与参数方程在直角坐标系xOy中,以O为极点,x正半轴为极轴建立极坐标系,曲线C的极坐标方程为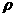 cos(
cos( )=1,M,N分别为C与x轴,y轴的交点。
)=1,M,N分别为C与x轴,y轴的交点。
(1)写出C的直角坐标方程,并求M,N的极坐标;
(2)设MN的中点为P,求直线OP的极坐标方程。
解(Ⅰ)由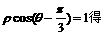

从而C的直角坐标方程为

(Ⅱ)M点的直角坐标为(2,0)
N点的直角坐标为
所以P点的直角坐标为
所以直线OP的极坐标方程为
9、 (09辽宁理22)(本小题满分10分)选修4-1:几何证明讲
(09辽宁理22)(本小题满分10分)选修4-1:几何证明讲
已知  ABC 中,AB=AC, D是
ABC 中,AB=AC, D是  ABC外接圆劣弧
ABC外接圆劣弧 上
上
的点(不与点A,C重合),延长BD至E。
(1)求证:AD的延长线平分 CDE;
CDE;
(2)若 BAC=30,
BAC=30, ABC中BC边上的高为2+
ABC中BC边上的高为2+ ,求
,求 ABC
ABC
外接圆的面积。
解(Ⅰ)如图,设F为AD延长线上一点
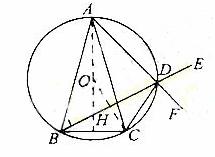 ∵A,B,C,D四点共圆,
∵A,B,C,D四点共圆,
∴∠CDF=∠ABC
又AB=AC ∴∠ABC=∠ACB,
且∠ADB=∠ACB, ∴∠ADB=∠CDF,
对顶角∠EDF=∠ADB, 故∠EDF=∠CDF,
即AD的延长线平分∠CDE.
(Ⅱ)设O为外接圆圆心,连接AO交BC于H,则AH⊥BC.
连接OC,A由题意∠OAC=∠OCA=150, ∠ACB=750,
∴∠OCH=600.
设圆半径为r,则r+ r=2+
r=2+ ,a得r=2,外接圆的面积为4
,a得r=2,外接圆的面积为4 。
。
8、(09江苏)A.选修4 - 1:几何证明选讲
如图,在四边形ABCD中,△ABC≌△BAD.
求证:AB∥CD.
[解析] 本小题主要考查四边形、全等三角形的有关知识,
 考查推理论证能力。满分10分。
考查推理论证能力。满分10分。
证明:由△ABC≌△BAD得∠ACB=∠BDA,故A、B、C、D四点共圆,从而∠CBA=∠CDB。再由△ABC≌△BAD得∠CAB=∠DBA。因此∠DBA=∠CDB,所以AB∥CD。
B. 选修4 - 2:矩阵与变换
求矩阵 的逆矩阵.
的逆矩阵.
[解析] 本小题主要考查逆矩阵的求法,考查运算求解能力。满分10分。
解:设矩阵A的逆矩阵为 则
则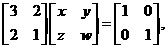
即 故
故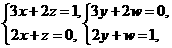
解得: ,
,
从而A的逆矩阵为 .
.
C. 选修4 - 4:坐标系与参数方程
已知曲线C的参数方程为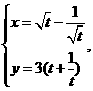 (
(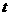 为参数,
为参数, ).
).
求曲线C的普通方程。
[解析]本小题主要考查参数方程和普通方程的基本知识,考查转化问题的能力。满分10分。
解 因为 所以
所以
故曲线C的普通方程为: .
.
D. 选修4 - 5:不等式选讲
设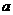 ≥
≥ >0,求证:
>0,求证: ≥
≥ .
.
证明:
因为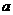 ≥
≥ >0,所以
>0,所以 ≥0,
≥0, >0,从而
>0,从而 ≥0,
≥0,
即 ≥
≥ .
.
7、(09海南24)(本小题满分10分)选修4-5:不等式选讲
如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,y 表示C到A距离4倍与C道B距离的6倍的和.
(1)将y表示成x的函数;
(2)要使y的值不超过70,x 应该在什么范围内取值?

解
(Ⅰ)
(Ⅱ)依题意,x满足
{
解不等式组,其解集为[9,23]
所以 
6、(09海南23)(本小题满分10分)选修4-4:坐标系与参数方程。
已知曲线C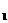 :
: (t为参数), C
(t为参数), C :
: (
( 为参数)。
为参数)。
(1)化C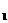 ,C
,C 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C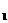 上的点P对应的参数为
上的点P对应的参数为 ,Q为C
,Q为C 上的动点,求
上的动点,求 中点
中点 到直线
到直线
 (t为参数)距离的最小值。
(t为参数)距离的最小值。
解:(Ⅰ)
 为圆心是(
为圆心是( ,半径是1的圆.
,半径是1的圆.
 为中心是坐标原点,焦点在x轴上,长半轴长是8,短半轴长是3的椭圆.
为中心是坐标原点,焦点在x轴上,长半轴长是8,短半轴长是3的椭圆.
(Ⅱ)当 时,
时,
 为直线
为直线
从而当 时,
时,
5、(09海南22)本小题满分10分)选修4-1:几何证明选讲
如图,已知 的两条角平分线
的两条角平分线 和
和 相交于H,
相交于H, ,F在
,F在 上,
上,
且 。
。
(Ⅰ)证明:B,D,H,E四点共圆:
(Ⅱ)证明: 平分
平分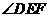 。
。
 解:(Ⅰ)在△ABC中,因为∠B=60°,
解:(Ⅰ)在△ABC中,因为∠B=60°,
所以∠BAC+∠BCA=120°.
因为AD,CE是角平分线,
所以∠HAC+∠HCA=60°,
故∠AHC=120°.
于是∠EHD=∠AHC=120°.
因为∠EBD+∠EHD=180°,
所以B,D,H,E四点共圆.
(Ⅱ)连结BH,则BH为∠ABC的平分线,得∠HBD=30°
由(Ⅰ)知B,D,H,E四点共圆,
所以∠CED=∠HBD=30°.
又∠AHE=∠EBD=60°,由已知可得EF⊥AD,
可得∠CEF=30°.
所以CE平分∠DEF.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com