
题目列表(包括答案和解析)
1.(2009番禺一模)在直角坐标系中圆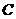 的参数方程为
的参数方程为
 (
( 为参数),若以原点
为参数),若以原点 为极点,以
为极点,以 轴正半轴为极轴建立极坐标系,则圆
轴正半轴为极轴建立极坐标系,则圆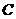 的极坐标方程为______ __.
的极坐标方程为______ __.
答案 
4.(三明市三校联考)本题(1)、(2)、(3)三个选答题,每小题7分,请考生任选2题作答,满分14分,如果多做,则按所做的前两题计分。
(Ⅰ)(本小题满分7分)选修4-4:矩阵与变换
求矩阵 的逆矩阵.
的逆矩阵.
(Ⅱ)(本小题满分7分)选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: ,求直线l与曲线C相交所成的弦的弦长.
,求直线l与曲线C相交所成的弦的弦长.
(Ⅲ)(本小题满分7分)选修4-5:不等式选讲
解不等式∣2x-1∣<∣x∣+1
解: (I) 设矩阵A的逆矩阵为 则
则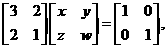
即 故
故
解得: ,
,
从而A的逆矩阵为 .
.
(Ⅱ)曲线C的极坐标方程是 化为直角坐标方程为x2+y2-4x=0,即(x-2)2+y2=4
化为直角坐标方程为x2+y2-4x=0,即(x-2)2+y2=4
直线l的参数方程 ,化为普通方程为x-y-1=0, 曲线C的圆心(2,0)到直线l的距离为
,化为普通方程为x-y-1=0, 曲线C的圆心(2,0)到直线l的距离为
所以直线l与曲线C相交所成的弦的弦长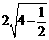 =
= .
.
(Ⅲ)当x<0时,原不等式可化为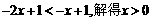 又
又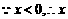 不存在;
不存在;
当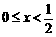 时,原不等式可化为
时,原不等式可化为 ;又
;又
当
综上,原不等式的解集为
3. (哈师大附中、东北师大附中、辽宁省实验中学)(本小题满分10分)
选修4-5:不等式选讲
对于任意实数
 和
和 ,不等式
,不等式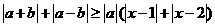 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
解:由题知,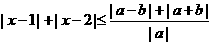 恒成立,
恒成立,
故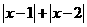 不大于
不大于 的最小值 …………
的最小值 …………
∵ ,当且仅当
,当且仅当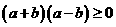 时取等号
时取等号
∴ 的最小值等于2. …………
的最小值等于2. …………
∴x的范围即为不等式|x-1|+|x-2|≤2的解
…………
解不等式得 …………
…………
2. (哈师大附中、东北师大附中、辽宁省实验中学)
(本小题满分10分)选修4-4:坐标系与参数方程
在极坐标系下,已知圆O: 和直线
和直线 ,
,
(1)求圆O和直线 的直角坐标方程;
的直角坐标方程;
(2)当 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
解:(1)圆O: ,即
,即
圆O的直角坐标方程为: ,即
,即 …………
…………
直线 ,即
,即
则直线 的直角坐标方程为:
的直角坐标方程为: ,即
,即 …………
…………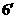
(2)由 得
得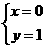

故直线 与圆O公共点的一个极坐标为
与圆O公共点的一个极坐标为 …………
…………
1.(哈师大附中、东北师大附中、辽宁省实验中学)(本小题满分10分)
选修4-1:几何证明选讲
如图,⊙ 的直径
的直径 的延长线与弦
的延长线与弦 的延长线相交于点
的延长线相交于点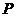 ,
,
 为⊙
为⊙ 上一点,AE=AC
,
上一点,AE=AC
,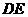 交
交 于点
于点 ,且
,且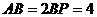 ,
,
 (1)求
(1)求 的长度.
的长度.
(2)若圆F且与圆 内切,直线PT与圆F切于点T,求线段PT的长度
内切,直线PT与圆F切于点T,求线段PT的长度
解:(1)连结 ,由同弧对应的圆周角与圆心角之间的关系
,由同弧对应的圆周角与圆心角之间的关系
结合题中条件弧长 等于弧长
等于弧长 可得
可得 ,
,
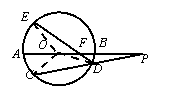 又
又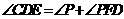 ,
,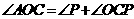 ,
,
从而 ,故
,故 ∽
∽ ,∴
,∴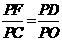 ,
…………
,
…………
由割线定理知 ,故
,故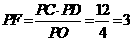 . ………
. ………
(2)若圆F与圆 内切,设圆F的半径为r,因为
内切,设圆F的半径为r,因为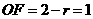 即
即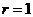
所以 是圆F的直径,且过P点圆F的切线为PT
是圆F的直径,且过P点圆F的切线为PT
则 ,即
,即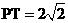 …………
…………
2010年联考题
7. (2008江苏)A.选修4-1:几何证明选讲
(2008江苏)A.选修4-1:几何证明选讲
如图所示,设△ABC的外接圆的切线AE与BC的延长线
交于点E,∠BAC的平分线与BC交于点D.求证:ED2=EC·EB.
B.选修4-2:矩阵与变换
在平面直角坐标系xOy中,设椭圆4x2+y2=1在矩阵A= 对应的变换下得到曲线F,求F的方程.
对应的变换下得到曲线F,求F的方程.
C:选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,设P(x,y)是椭圆 上的一个动点,
上的一个动点,
求S=x+y的最大值.
D:选修4-5:不等式选讲
设a,b,c为正实数,求证: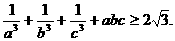
A.证明: 如图所示,因为AE是圆的切线,
 又因为AD是∠BAC的平分线,
又因为AD是∠BAC的平分线,
所以∠BAD=∠CAD.
从而∠ABC+∠BAD=∠CAE+∠CAD.
因为∠ADE=∠ABC+∠BAD,∠DAE=∠CAE+∠CAD,
所以∠ADE=∠DAE,故EA=ED.
因为EA是圆的切线,所以由切割线定理知,EA2=EC·EB, 而EA=ED,所以ED2=EC·EB.
B.解: 设P(x0,y0)是椭圆上任意一点,
点P(x0,y0)在矩阵A对应的变换下变为点P′(x′0,y′0),则有
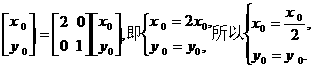
又因为点P在椭圆上,故
所以曲线F的方程为
C.解:由椭圆

故可设动点P的坐标为(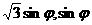 ),其中
),其中
因此,
所以当
D.证明:因为a,b,c是正实数,由平均不等式可得


所以
6.(2008宁夏理)(10分)选修4-5:不等式选讲
已知函数 .
.
(1)作出函数 的图象;
的图象;
(2)解不等式 .
.
解(1)
图象如下:

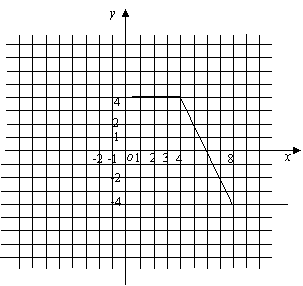

(2)不等式 ,即
,即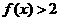 ,
,
由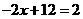 得
得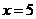 .
.
由函数 图象可知,原不等式的解集为
图象可知,原不等式的解集为 .
.
5.(2008宁夏理)(10分)选修4-4:坐标系与参数方程选讲
已知曲线C1: ,曲线C2:
,曲线C2: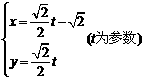 .
.
(1)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线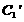 ,
, .写出
.写出
 ,
, 的参数方程.
的参数方程. 与
与 公共点的个数和C1与C2公共点的个数是否相同?说
公共点的个数和C1与C2公共点的个数是否相同?说
明你的理由.
解(1) 是圆,
是圆, 是直线.
是直线.
 的普通方程为
的普通方程为 ,圆心
,圆心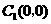 ,半径
,半径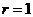 .
.
 的普通方程为
的普通方程为 .
.
因为圆心 到直线
到直线 的距离为
的距离为 ,
,
所以 与
与 只有一个公共点.
只有一个公共点.
(2)压缩后的参数方程分别为
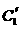 :
: (
( 为参数);
为参数);  :
: (t为参数).
(t为参数).
化为普通方程为: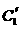 :
: ,
, :
: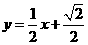 ,
,
联立消元得 ,
,
其判别式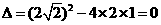 ,
,
所以压缩后的直线 与椭圆
与椭圆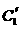 仍然只有一个公共点,和
仍然只有一个公共点,和 与
与 公共点个数相同.
公共点个数相同.
4. (2008宁夏理)(10分)选修4-1:几何证明选讲
(2008宁夏理)(10分)选修4-1:几何证明选讲
如图,过圆O外一点M作它的一条切线,切点为A,
过A作直线AP垂直于直线OM,垂足为P.
(1)证明:OM·OP = OA2;
(2)N为线段AP上一点,直线NB垂直于直线ON,
且交圆O于B点.过B点的切线
交直线ON于K.证明:∠OKM = 90°.
(1)证明 因为 是圆
是圆 的切线,所以
的切线,所以 .
.
又因为 .在
.在 中,由射影定理知,
中,由射影定理知,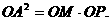
(2)证明 因为 是圆
是圆 的切线,
的切线, .
.
同(1),有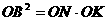 ,又
,又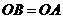 ,
,
所以 ,即
,即 .
.
又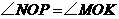 ,
,
所以 ,故
,故 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com