
题目列表(包括答案和解析)
44、(2009厦门乐安中学)(极坐标与参数方程)在极坐标系中,设圆 上的点到直线
上的点到直线 的距离为
的距离为 ,求
,求 的最大值.
的最大值.
解 将极坐标方程 转化为普通方程:
转化为普通方程:
 可化为
可化为
在 上任取一点A
上任取一点A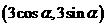 ,则点A到直线的距离为
,则点A到直线的距离为
 ,它的最大值为4
,它的最大值为4
43、(2009厦门集美中学)(极坐标与参数方程)求曲线 过点
过点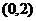 的切线方程.
的切线方程.
 ,消去参数
,消去参数 得
得 .
.
设切线为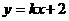 ,代入得
,代入得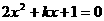
令 ,得
,得 ,故
,故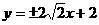 即为所求.
即为所求.
或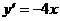 ,设切点为
,设切点为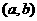 ,则斜率为
,则斜率为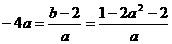 ,解得
,解得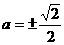 ,
,
即得切线方程.
42、(2009厦门二中)(极坐标与参数方程)已知直线 的参数方程:
的参数方程: (
( 为参
为参
数),圆C的极坐标方程: ,试判断直线
,试判断直线 与圆C的位置关系.
与圆C的位置关系.
解 将直线 的参数方程化为普通方程为:
的参数方程化为普通方程为: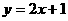
将圆C的极坐标方程化为普通方程为:
从圆方程中可知:圆心C(1,1),半径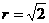 ,
,
所以,圆心C到直线 的距离
的距离
所以直线 与圆C相交.
与圆C相交.
41、(2009厦门一中)(极坐标与参数方程)已知直线 经过点
经过点 ,倾斜角
,倾斜角 ,设
,设 与曲线
与曲线 (
( 为参数)交于两点
为参数)交于两点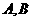 ,求点
,求点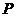 到
到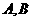 两点的距离之积。
两点的距离之积。
解 直线的参数方程为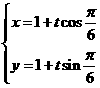 ,即
,即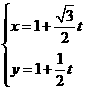
曲线的直角坐标方程为 ,把直线
,把直线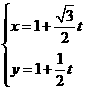 代入
代入
得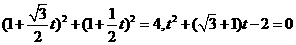
 ,则点
,则点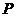 到
到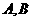 两点的距离之积为
两点的距离之积为
40、(2009厦门同安一中)(矩阵)在直角坐标系中,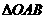 的顶点坐标
的顶点坐标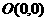 ,
, ,
, ,求
,求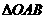 在矩阵
在矩阵 的作用下变换所得到的图形的面积,其中矩阵
的作用下变换所得到的图形的面积,其中矩阵 ,
,
解 ,
,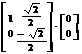
 …2分
…2分 ……4分.
……4分.
 ……5分
……5分
可知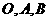 三点在矩阵
三点在矩阵 作用下变换所得的点分别为
作用下变换所得的点分别为 .
.
可得 的面积为1.……7分.
的面积为1.……7分.
39、(2009厦门十中)(矩阵)已知矩阵A= ,B=
,B=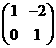 .
.
①计算AB;
②若矩阵B把直线 变为直线
变为直线 ,求直线
,求直线 的方程.
的方程.
解 ①AB=
②任取直线 上一点P(x,y),设P经矩阵B变换后为
上一点P(x,y),设P经矩阵B变换后为 ,则
,则
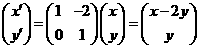 ,
,
代入 ,得
,得 ,∴直线
,∴直线 的方程为
的方程为 .
.
38、(2009厦门乐安中学)(矩阵)已知矩阵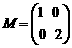 ,
, ,矩阵
,矩阵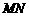 对应的变换把曲线
对应的变换把曲线 变为曲线C,求C的方程.
变为曲线C,求C的方程.
解
 ,设
,设 是所求曲线C上的任意一点,它是曲线
是所求曲线C上的任意一点,它是曲线
 上点
上点 在矩阵
在矩阵 变换下的对应点,则有
变换下的对应点,则有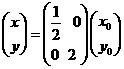 ,即
,即 所以
所以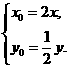 又点
又点 在曲线
在曲线 上,故
上,故 ,从而
,从而 ,所求曲线C的方程为
,所求曲线C的方程为 .
.
37、(2009厦门英才学校)(不等式选讲)已知函数 .
.
(Ⅰ)作出函数 的图像;
的图像;
(Ⅱ)解不等式
解 (Ⅰ)依题意可知
(Ⅰ)依题意可知 ,
,
则函数 的图像如图所示:
的图像如图所示:
(Ⅱ)由函数 的图像容易求得原不等式的
的图像容易求得原不等式的
解集为 …………7分
…………7分
36、(2009厦门同安一中)(不等式选讲)已知 、
、 ,且
,且 ,求
,求
的最小值
解 因为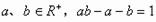 ,所以
,所以 ,所以
,所以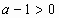 ,
,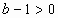 ,所以
,所以 。式中等号当且仅当
。式中等号当且仅当 时成立,此时
时成立,此时 。所以当
。所以当 时,
时, 取最小值
取最小值 .
.
35、(2009厦门十中)(不等式选讲)已知实数
 满足
满足 ,
,  试求
试求 的最值
的最值
解 由柯西不等式得,有
即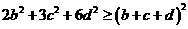 由条件可得,
由条件可得, 
解得,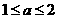 当且仅当
当且仅当 时等号成立,
时等号成立,
代入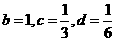 时,
时, 
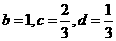 时
时 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com