
题目列表(包括答案和解析)
3.(2009安徽卷文)不等式组 所表示的平面区域的面积等于
A.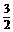 B.
B. C.
C.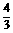 D.
D.
解析 由 可得
可得 ,故
,故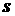 阴 =
阴 = ,选C。
,选C。
答案 C
2.(2009安徽卷理)若不等式组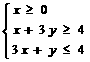 所表示的平面区域被直线
所表示的平面区域被直线 分为面积相等的两部分,则
分为面积相等的两部分,则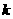 的值是
的值是
A. B.
B. 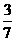 C.
C. D.
D. 
答案 B
 解析 不等式表示的平面区域如图所示阴影部分△ABC
解析 不等式表示的平面区域如图所示阴影部分△ABC
由 得A(1,1),又B(0,4),C(0,
得A(1,1),又B(0,4),C(0, )
)
∴ △ABC=
△ABC= ,设
,设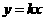 与
与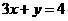 的
的
交点为D,则由 知
知 ,∴
,∴
 ∴
∴ 选A。
选A。
1. (2009山东卷理)设x,y满足约束条件
(2009山东卷理)设x,y满足约束条件 ,
,
若目标函数z=ax+by(a>0,b>0)的是最大值为12,
则 的最小值为 ( ).
的最小值为 ( ).
A. B.
B. C.
C. 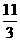 D.
4
D.
4
答案 A
解析 不等式表示的平面区域如图所示阴影部分,当直线ax+by= z(a>0,b>0)
过直线x-y+2=0与直线3x-y-6=0的交点(4,6)时,
目标函数z=ax+by(a>0,b>0)取得最大12,
即4a+6b=12,即2a+3b=6, 而 =
= ,故选A.
,故选A.
[命题立意]:本题综合地考查了线性规划问题和由基本不等式求函数的最值问题.要求能准确地画出不等式表示的平面区域,并且能够求得目标函数的最值,对于形如已知2a+3b=6,求 的最小值常用乘积进而用基本不等式解答.
的最小值常用乘积进而用基本不等式解答.
4.(2009湖北卷文)(本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
解:(1)如图,设矩形的另一边长为a m
则 -45x-180(x-2)+180·2a=225x+360a-360
-45x-180(x-2)+180·2a=225x+360a-360
由已知xa=360,得a= ,
,
所以y=225x+
(II)

 .当且仅当225x=
.当且仅当225x=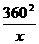 时,等号成立.
时,等号成立.
即当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
第三节 不等式组与简单的线性规划
3.(2009湖南卷文)若 ,则
,则 的最小值为
.
的最小值为
.
答案  2
2
解析 
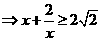 ,当且仅当
,当且仅当 时取等号.
时取等号.
2.(2009重庆卷文)已知 ,则
,则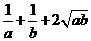 的最小值是( )
的最小值是( )
A.2 B. C.4 D.5
C.4 D.5
答案 C
解析 因为 当且仅当
当且仅当 ,且 ,即
,且 ,即 时,取“=”号。
时,取“=”号。
1.(2009天津卷理)设 若
若 的最小值为
的最小值为
A . 8 B . 4 C.
1 D. 
考点定位 本小题考查指数式和对数式的互化,以及均值不等式求最值的运用,考查了变通能力。
答案 C
解析 因为 ,所以
,所以 ,
,
 ,当且仅当
,当且仅当 即
即 时“=”成立,故选择C
时“=”成立,故选择C
7.(2009年上海卷理)若行列式 中,元素4的代数余子式大于0,
中,元素4的代数余子式大于0,
则x满足的条件是________________________ .
答案

解析 依题意,得: (-1)2×(9x-24)>0,解得:
6.(2009重庆卷理)不等式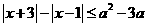 对任意实数
对任意实数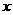 恒成立,则实数
恒成立,则实数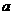 的取值范围为( )
的取值范围为( )
A. B.
B.
C.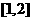 D.
D.
答案 A
解析 因为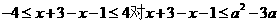 对任意x恒成立,所以
对任意x恒成立,所以
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com