
题目列表(包括答案和解析)
1、(2008山东)设二元一次不等式组 所表示的平面区域为M,使函数y=ax(a>0,a≠1)的图象过区域M的a的取值范围是( )
所表示的平面区域为M,使函数y=ax(a>0,a≠1)的图象过区域M的a的取值范围是( )
A .[1,3]
B.[2, C.[2,9]
C.[2,9]
D.[ ,9]
,9]
答案 C
解析 本题考查线性规划与指数函数。如图阴影部分为平面区域M, 显然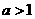 ,只需
,只需
研究过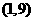 、
、 两种情形。
两种情形。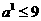 且
且 即
即

15.(2006上海春)已知直线 过点
过点 ,且与
,且与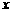 轴、
轴、 轴的正半轴分别交于
轴的正半轴分别交于 两点,
两点, 为坐标原点,则三角形
为坐标原点,则三角形 面积的最小值为 .
面积的最小值为 .
答案 4
解析 设直线 l 为  ,则有关系
,则有关系 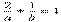 .
对
.
对  应用2元均值不等式,得
应用2元均值不等式,得  ,即ab≥8 .于是,△OAB 面积为
,即ab≥8 .于是,△OAB 面积为  .从而应填4.
.从而应填4.
第三节 不等式组与简单的线性规划
14.(2006天津)某公司一年购买某种货物400吨,每次都购买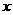 吨,运费为4万元/次,一年的总存储费用为
吨,运费为4万元/次,一年的总存储费用为 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则 _______
吨.
_______
吨.
解析 某公司一年购买某种货物400吨,每次都购买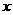 吨,则需要购买
吨,则需要购买 次,运费为4万元/次,一年的总存储费用为
次,运费为4万元/次,一年的总存储费用为 万元,一年的总运费与总存储费用之和为
万元,一年的总运费与总存储费用之和为 万元,
万元, ≥160,当
≥160,当 即
即 20吨时,一年的总运费与总存储费用之和最小。
20吨时,一年的总运费与总存储费用之和最小。
答案 2
13.(2006上海)三个同学对问题“关于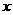 的不等式
的不等式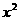 +25+|
+25+| -5
-5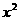 |≥
|≥ 在[1,12]上恒成立,求实数
在[1,12]上恒成立,求实数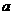 的取值范围”提出各自的解题思路.
的取值范围”提出各自的解题思路.
甲说:“只须不等式左边的最小值不小于右边的最大值”.
乙说:“把不等式变形为左边含变量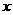 的函数,右边仅含常数,求函数的最值”.
的函数,右边仅含常数,求函数的最值”.
丙说:“把不等式两边看成关于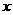 的函数,作出函数图像”.
的函数,作出函数图像”.
参考上述解题思路,你认为他们所讨论的问题的正确结论,即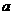 的取值范围
的取值范围
是 .
解析 由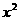 +25+|
+25+| -5
-5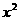 |≥
|≥ ,而
,而
 ,等号当且仅当
,等号当且仅当 时成立;且
时成立;且 ,等号当且仅当
,等号当且仅当 时成立;所以,
时成立;所以, ,等号当且仅当
,等号当且仅当 时成立;故
时成立;故 ;
;
答案(-∞,10)
12.(2007山东)函数y=loga(x+3)-1(a>0,a 1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中mn>0,则
1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中mn>0,则 的最小值为
.
的最小值为
.
答案 8
11.(2007上海)已知 ,且
,且 ,则
,则 的最大值为
的最大值为
答案

10.(2008江苏)已知 ,
,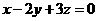 ,则
,则 的最小值
.
的最小值
.
答案 3
9、(2009韶关一模)①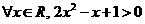 ;②“
;②“ 且
且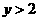 ”是“
”是“ ”的充要条件;③ 函数
”的充要条件;③ 函数 的最小值为
的最小值为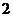
其中假命题的为_________(将你认为是假命题的序号都填上)
答案 ①
8、(2009广东三校一模)若直线 通过点
通过点 ,则
,则
A.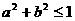
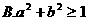


答案 B
7.(2006重庆)若a,b,c>0且a(a+b+c)+bc=4-2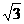 ,则2a+b+c的最小值为
,则2a+b+c的最小值为
A.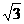 -1 B.
-1 B. 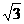 +1
C. 2
+1
C. 2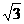 +2
D. 2
+2
D. 2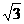 -2
-2
答案 D
解析 若 且
且 所以
所以 ,
, ∴
∴
 ,则(
,则( )≥
)≥ ,选D.
,选D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com