4．(2010年皖南八校联考)两个正数a，b的等差中项是5，等比中项是4.若a＞b，则双曲线－＝1的渐近线方程是________．

解析：由已知得⇒(a＞b)．

故双曲线的渐近线方程为y＝± x＝±x.

答案：y＝±x

3．(2009年高考四川卷)已知双曲线－＝1(b＞0)的左、右焦点分别为F₁、F₂，其一条渐近线方程为y＝x，点P(，y₀)在该双曲线上，则·＝(　)

A．－12　 　　　　　　　　　B．－2

C．0　 　　　　　　　　　　D．4

解析：选C.∵渐近线方程为y＝x，∴b²＝2.

又P(，y₀)在双曲线上，∴y₀²＝1.又∵F₁(－2,0)，F₂(2,0)，

∴·＝(－2－，－y₀)·(2－，－y₀)

＝3－4+y₀²＝0.

2．(原创题)若k∈R，则“k＞3”是“方程－＝1表示双曲线”的(　)

A．充分不必要条件 　　　　　B．必要不充分条件

C．充要条件　 　　　　　　　D．既不充分也不必要条件

解析：选A.若方程表示双曲线，则(k－3)(k+3)＞0，

∴k＜－3或k＞3，

故k＞3是方程表示双曲线的充分不必要条件．

1．方程ax²+by²＝c表示双曲线是ab<0的(　)

A．充分非必要条件

B．必要非充分条件

C．充要条件

D．既不充分也不必要条件

解析：选A.方程ax²+by²＝c表示双曲线，则a，b异号，反之若a＝1，b＝－1，c＝0，则不能表示双曲线．

12．如图是解决某个问题而绘制的程序框图，仔细分析各图框内的内容及图框之间的关系，回答下面的问题：

(1)图框①中x＝2的含义是什么？

(2)图框②中y₁＝ax+b的含义是什么？

(3)图框④中y₂＝ax+b的含义是什么？

(4)该程序框图解决的是怎样的一个问题？

(5)若最终输出的结果是y₁＝3，y₂＝－2，当x取5时输出的结果5a+b的值应该是多大？

(6)在(5)的前提下输入的x值越大，输出结果ax+b是不是越大？为什么？

(7)在(5)的前提下当输入的x值为多大，输出结果ax+b等于0?

解：(1)图框①中x＝2表示把2赋给变量x或使x＝2.

(2)图框②中y₁＝ax+b的含义：该图框在执行①的前提下，即当x＝2时计算ax+b的值，并把这个值赋给y₁.

(3)图框④中，y₂＝ax+b的含义：该图框在执行③的前提下，即当x＝－3时计算ax+b的值，并把这个值赋给y₂.

(4)该程序框图解决的是求函数f(x)＝ax+b的函数值的问题，其中输入的是自变量x的值，输出的是x对应的函数值．

(5)y₁＝3，即2a+b＝3.(i)

y₂＝－2，即－3a+b＝－2(ii)

由(i)(ii)得a＝1，b＝1，

∴f(x)＝x+1.

∴x取5时，5a+b＝f(5)＝5×1+1＝6，

(6)输入的x值越大，输出的函数值ax+b越大，因为f(x)＝x+1是R上的增函数．

(7)令f(x)＝x+1＝0得x＝－1，因而当输入的值为－1时，输出的函数值为0.

11．某居民区的物业管理部门每月向居民收取卫生费，计费方法如下：3人和3人以下的住户，每户收取5元；超过3人的住户，每超出1人加收1.2元．设计一个算法，根据输入的人数，计算应收取的卫生费只需画出程序框图即可．

解：依题意得，费用y与人数n之间的关系为：

y＝.

程序框图如下图所示：

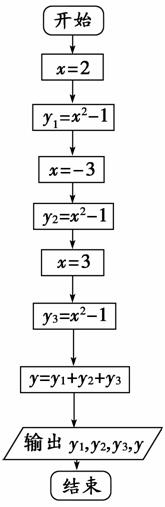
10．已知f(x)＝x²－1，求f(2)，f(－3)，f(3)，并计算f(2)+f(－3)+f(3)的值，设计出解决该问题的一个算法，并画出程序框图．

解：算法如下：

第一步：x＝2；

第二步：y₁＝x²－1；

第三步：x＝－3；

第四步：y₂＝x²－1；

第五步：x＝3；

第六步：y₃＝x²－1；

第七步：y＝y₁+y₂+y₃；

第八步：输出y₁，y₂，y₃，y.

程序框图：

9．下图是一个算法的流程图，最后输出的W＝________.

解析：由流程图知，第一次循环：T＝1，S＝1；

第二次循环：T＝3，S＝3²－1＝8；

第三次循环：T＝5，S＝5²－8＝17，

此时跳出循环，∴W＝5+17＝22.

答案：22

8．定义某种运算S＝a⊗b，运算原理如图所示．

则式子：(2tan)⊗lne+lg100⊗()^－1的值是________．

解析：原式＝2⊗1+2⊗3＝2×(1+1)+2×(3－1)＝8.

答案：8

7．如图所给出的是计算+++…+的值的一个程序框图，其中判断框内应填入的条件是________．

解析：由框图知，要经过10次循环才能算出此表达式的值，

∴应填入“i>10？”．

答案：i>10?