6．(2008年高考天津卷)已知函数f(x)是定义在R上的偶函数，且在区间[0，+∞)上是增函数．令a＝f(sin)，b＝f(cos)，c＝f(tan)，则(　)

A．b＜a＜c　 　　　　　　　　　B．c＜b＜a

C．b＜c＜a　 　　　　　　　　　D．a＜b＜c

解析：选A.sinπ＝sin(π－π)＝sinπ.

又＜π＜π.

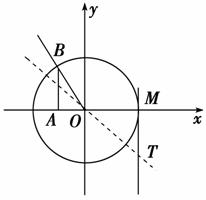由三角函数线tanπ＜cosπ＜sinπ且cosπ＜0，

sinπ＞0.如图．

∴＜＜.

又f(x)在[0，+∞)上递增且为偶函数，

∴f()＜f()＜f()，

即b＜a＜c，故选A.

5．已知函数y＝2sin²(x+)－cos2x，则它的周期T和图象的一条对称轴方程是(　)

A．T＝2π，x＝　 　　　　　　B．T＝2π，x＝

C．T＝π，x＝　 　　　　　　　D．T＝π，x＝

解析：选D.∵y＝2sin²(x+)－cos2x＝1－cos(2x+)－cos2x＝1+sin2x－cos2x＝1+sin(2x－)，所以其周期T＝π，对称轴方程的表达式可由2x－＝kπ+(k∈Z)得x＝+(k∈Z)，故当k＝0时的一条对称轴方程为x＝，故答案为D.

4．设点P是函数f(x)＝sinωx的图象C的一个对称中心，若点P到图象C的对称轴的距离的最小值是，则f(x)的最小正周期是(　)

A.　 　　　　　　　　　　　　B．π

C．2π　 　　　　　　　　　　　D.

解析：选A.依题意得＝，所以最小正周期为T＝.

3．(2009年高考重庆卷)下列关系式中正确的是(　)

A．sin11°<cos10°<sin168°　 　　B．sin168°<sin11°<cos10°

C．sin11°<sin168°<cos10°　 　　D．sin168°<cos10°<sin11°

解析：选C.∵sin168°＝sin(180°－12°)＝sin12°，

cos10°＝sin(90°－10°)＝sin80°.

又∵g(x)＝sinx在x∈[0，]上是增函数，

∴sin11°<sin12°<sin80°，即sin11°<sin168°<cos10°.

2．函数f(x)＝tanωx(ω>0)图象的相邻两支截直线y＝所得线段长为，则f()的值是(　)

A．0 　　　　　　　　　　　　B．1

C．－1 　　　　　　　　　　　D.

解析：选A.由题意知T＝ ，由＝得ω＝4，

∴f(x)＝tan4x，∴f()＝tanπ＝0.

1.函数y＝|sinx|－2sinx的值域是(　)

A．[－3，－1]　 　　　　　　　B．[－1,3]

C．[0,3]　 　　　　　　　　　　D．[－3,0]

解析：选B.当0≤sinx≤1时，y＝sinx－2sinx＝－sinx，此时y∈[－1,0]；当－1≤sinx<0时，y＝－sinx－2sinx＝－3sinx，此时y∈(0,3]，求其并集得y∈[－1,3]．

6．已知函数f(x)＝sin2x－2cos²x(x∈R)．

(1)求函数f(x)的最小正周期；

(2)当x∈[0，]时，求函数f(x)的最大值及相应的x值．

解：(1)f(x)＝sin2x－2cos²x＝sin2x－cos2x－1，

则f(x)＝sin(2x－)－1，

所以，函数f(x)的最小正周期为π.

(2)由x∈[0，]，得3x－∈[－，]，

当2x－＝，即x＝π时，f(x)有最大值－1.

练习

5．(原创题)若f(x)是以5为周期的函数，f(3)＝4，且cosα＝，则f(4cos2α)＝________.

解析：4cos2α＝4(2cos²α－1)＝－2.

∴f(4cos2α)＝f(－2)＝f(－2+5)＝f(3)＝4.

答案：4

4．函数y＝sin(－x)的单调递增区间为________．

解析：由y＝sin(－x)得y＝－sin(x－)，

由+2kπ≤x－≤π+2kπ，k∈Z，得

π+3kπ≤x≤+3kπ，k∈Z，

故函数的单调增区间为[π+3kπ，+3kπ](k∈Z)．

答案：[π+3kπ，+3kπ](k∈Z)

3．若函数y＝2cos(2x+φ)是偶函数，且在(0，)上是增函数，则实数φ可能是(　)

A．－ 　　　　　　　　　　　　　B．0

C.　 　　　　　　　　　　　　　　D．π

解析：选D.依次代入检验知，当φ＝π时，函数y＝2cos(2x+π)＝－2cos2x，此时函数是偶函数且在(0，)上是增函数．