2.函数y＝sin(2x－)在区间[－，π]上的简图是(　)

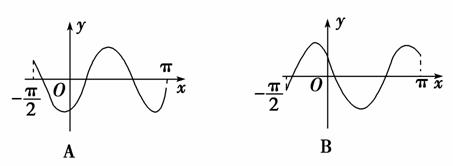
解析：选A.令x＝0得y＝sin(－)＝－，淘汰B，D.由f(－)＝0，f()＝0，淘汰C，故选A.

1．(2009年高考天津卷)已知函数f(x)＝sin(ωx+)(x∈R，ω>0)的最小正周期为π，为了得到函数g(x)＝cosωx的图象，只要将y＝f(x)的图象(　)

A．向左平移个单位长度

B．向右平移个单位长度

C．向左平移个单位长度

D．向右平移个单位长度

解析：选A.因为T＝π，则ω＝＝2，f(x)＝sin(2x+)，g(x)＝cos2x，将y＝f(x)的图象向左平移个单位长度时，y＝sin[2(x+)+]＝sin(2x+)＝cos2x.

6．已知函数f(x)＝sin²ωx+sinωxsin(ωx+)+2cos²ωx，x∈R(ω>0)，在y轴右侧的第一个最高点的横坐标为.

(1)求f(x)的对称轴方程；

(2)求f(x)的单调递增区间．

解：(1)f(x)＝sin2ωx+cos2ωx+

＝sin(2ωx+)+.

令2ωx+＝，将x＝代入可得：ω＝1，

f(x)＝sin(2x+)+，

对称轴方程为2x+＝kπ+(k∈Z)，

即x＝kπ+(k∈Z)．

(2)由2kπ－≤2x+≤2kπ+(k∈Z)可得

单调增区间为[kπ－，kπ+](k∈Z)．

练习

5．(2009年高考宁夏海南卷)已知函数f(x)＝2sin(ωx+φ)的图象如下图所示，则f()＝________.

解析：由图象知，函数的周期T满足×T＝π，∴T＝.

∵f()＝0，

∴f()＝f(+)

＝f(+)＝－f()＝0.

答案：0

4．(原创题)设函数y＝cosπx的图象位于y轴右侧所有的对称中心从左到右依次为A₁，A₂，…，A_n，…，则A₁₀的坐标是________．

解析：对称中心横坐标为x＝2k+1，k≥0，令k＝9得x＝19.

答案：(19,0)

3．函数f(x)＝3sin(2x－)的图象为C，下列结论中正确的是(　)

A．图象C关于直线x＝对称

B．图象C关于点(－，0)对称

C．函数f(x)在区间(－，)内是增函数

D．由y＝3sin2x的图象向右平移个单位长度可以得到图象C

解析：选C.选项A错误，由于f()＝0≠±3，故A错．选项B错误，由于正弦类函数图象的对称点是图象的平衡点，因为f(－)＝3sin(－2×－)＝－，所以(－，0)不在函数图象上．此函数图象不关于这点对称，故B错误．选项C正确，令u＝2x－，当－<x<时，－<u<，由于y＝3sinu在(－，)上是增函数，所以选项C正确．选项D错误，由于y＝3sin2x的图象向右平移个单位得y＝3sin2(x－)即y＝3sin(2x－)的图象而不是图象C.综上，本题选C.

2．(2009年高考湖南卷)将函数y＝sinx的图象向左平移φ(0≤φ<2π)个单位后，得到函数y＝sin(x－)的图象，则φ等于(　)

A. 　　　　　　　　　　　　　B.

C. 　　　　　　　　　　　　D.

解析：选D.将函数y＝sinx向左平移φ(0≤φ<2π)个单位得到函数y＝sin(x+φ)．在A、B、C、D四项中，只有φ＝π时有y＝sin(x+π)＝sin(x－)．

1．(2008年高考全国卷Ⅱ)若动直线x＝a与函数f(x)＝sinx和g(x)＝cosx的图象分别交于M、N两点，则|MN|的最大值为(　)

A．1　 　　　　　　　　　　　　B.

C.　 　　　　　　　　　　　　D．2

解析：选B.|MN|＝|sina－cosa|＝，

∴|MN|_max＝，故选B.

8．已知函数f(x)＝2sinωx(ω>0)在区间[－，]上的最小值是－2，则ω的最小值等于________．

解析：由题意知≤，T＝，∴2ω≥3，ω≥，

∴ω的最小值等于.

7．函数y＝lgsinx+ 的定义域为________．

解析：(1)要使函数有意义必须有，

即，

解得(k∈Z)，

∴2kπ<x≤+2kπ，k∈Z，

∴函数的定义域为{x|2kπ<x≤+2kπ，k∈Z}．

答案：{x|2kπ<x≤+2kπ，k∈Z}