3.(2008年高考湖南卷)设D、E、F分别是△ABC的三边BC、CA、AB上的点，且＝2，＝2，＝2，则++与(　)

A．反向平行　 　　　　　　　　B．同向平行

C．互相垂直　 　　　　　　　　D．既不平行也不垂直

解析：选A.＝+＝+，＝+＝+，＝+＝+，

∴++＝++

＝(+)+

＝+＝－.故选A.

2．设a，b是任意的两个向量，λ∈R，给出下面四个结论：

①若a与b共线，则b＝λa.

②若b＝－λa，则a与b共线．

③若a＝λb，则a与b共线．

④当b≠0时，a与b共线的充要条件是有且只有一个实数λ＝λ₁，使得a＝λ₁b.

其中，正确的结论有(　)

A．①②　 　　　　　　　　　　B．①③

C．①③④　 　　　　　　　　　D．②③④

解析：选D.①a＝0，b≠0时，不成立，②③④均正确．

1．下列结论中，不正确的是(　)

A．向量，共线与向量∥同义

B．若向量∥，则向量与共线

C．若向量＝，则向量＝

D．只要向量a，b满足|a|＝|b|，就有a＝b

解析：选D.根据平行向量(或共线向量)定义知A、B均正确；根据向量相等的概念知C正确，D不正确．

6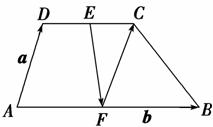．如图，已知梯形ABCD中，AB∥CD，且AB＝2CD，E、F分别是DC、AB的中点，设＝a，＝b，试用a，b表示，，.

解：∵DC∥AB，AB＝2DC，E、F分别是DC、AB的中点，

∴＝＝a，＝＝＝b.

＝++

＝－－+

＝－×b－a+b＝b－a.

练习

5．(原创题)设a，b是两个不共线的向量，若＝2a+kb，＝a+b，＝2a－b，且A，B，D三点共线，则实数k的值等于________．

解析：由于A，B，D三点共线，故∥，又＝2a+kb，＝－＝a－2b，故由2a+kb＝λ(a－2b)可解得k＝－4.

答案：－4

4．已知平面上不共线的四点O，A，B，C.若－3+2＝0，则等于________．

解析：由已知得：(－)+2(－)＝+2＝0⇒＝2，根据数乘的意义可得：＝2.

答案：2

3．已知O、A、B是平面上的三个点，直线AB上有一点C，满足2+＝0，则＝(　)

A．2－　 　　　　　　　　B．－+2

C.－　 　　　　　　　　D．－+

解析：选A.＝+＝+2

＝+2(－)，

∴＝2－.故选A.

2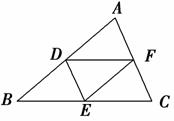．(2009年高考湖南卷)如图，D、E、F分别是△ABC的边AB、BC、CA的中点，则(　)

A.++＝0

B.－+＝0

C.+－＝0

D.－－＝0

解析：选A.++＝++＝(++)＝0.

1．若O、E、F是不共线的任意三点，则以下各式中成立的是(　)

A.＝+　 　　　　　　B.＝－

C.＝－+ 　　　　　　D.＝－－

解析：选B.由减法的定义可知＝－，B项正确．

5．(2009年高考安徽卷)在平行四边形ABCD中，E和F分别是边CD和BC的中点，若＝λ+μ，其中λ、μ∈R，则λ+μ＝________.

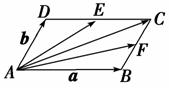解析：设＝a，＝b，

那么＝a+b，＝a+b，

又∵＝a+b，

∴＝(+)，即λ＝μ＝，

∴λ+μ＝.