1．(原创题)抛物线y²＝24ax(a＞0)上有一点M，它的横坐标是3，它到焦点的距离是5，则抛物线的方程为(　)

A．y²＝8x　 　　　　　　B．y²＝12x

C．y²＝16x　 　　　　　　D．y²＝20x

解析：选A.由题意知，3+6a＝5，∴a＝，

∴抛物线方程为y²＝8x.

12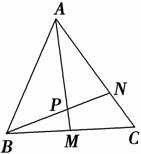．如图所示，在△ABC中，点M是BC的中点，点N在边AC上，且AN＝2NC，AM与BN相交于点P，求AP∶PM的值．

解：设＝e₁，＝e₂，

则＝+＝－3e₂－e₁，

＝2e₁+e₂

∵A、P、M和B、P、N分别共线，

∴存在实数λ、μ使

＝λ＝－λe₁－3λe₂，＝μ＝2μe₁+μe₂，

故＝－＝(λ+2μ)e₁+(3λ+μ)e₂.

而＝+＝2e₁+3e₂

∴解得

故＝，即AP∶PM＝4∶1.

11.设i、j分别是平面直角坐标系Ox，Oy正方向上的单位向量，且＝－2i+mj，＝ni+j，＝5i－j，若点A、B、C在同一条直线上，且m＝2n，求实数m、n的值．

解：＝－＝(n+2)i+(1－m)j，

＝－＝(5－n)i+(－2)j.

∵点A、B、C在同一条直线上，∴∥，

即＝λ，

∴(n+2)i+(1－m)j＝λ[(5－n)i+(－2)j]，

∴，解得或.

10．如图所示，D、E分别是△ABC中AB、AC边中点，M、N分别是DE、BC的中点，已知＝a，＝b，试用a、b分别表示、和.

解：由三角形中位线定理知DE綊BC.

故＝，即＝a.

＝++

＝－a+b+a＝－a+b.

＝++

＝++

＝－a－b+a＝a－b.

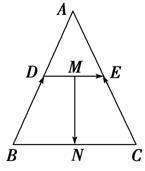
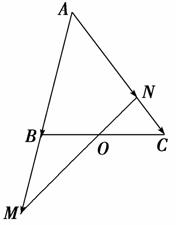
9．如图，在△ABC中，点O是BC的中点，过点O的直线分别交直线AB、AC于不同的两点M、N，若＝m，＝n，则m+n的值为________．

解析：＝(+)

＝+，

∵M，O，N三点共线，∴+＝1，

∴m+n＝2.

答案：2

8．设e₁，e₂是不共线向量，e₁－4e₂与ke₁+e₂共线，则实数k的值为________．

解析：由题意e₁－4e₂＝λ(ke₁+e₂)＝kλe₁+λe₂，

∴　∴k＝－.

答案：－

7．已知a与b是两个不共线向量，且向量a+λb与－(b－3a)共线，则λ＝________.

解析：由已知得a+λb＝－k(b－3a)，

∴，解得.

答案：－

6．设两个向量a＝(λ+2，λ²－cos²α)，b＝(m，+sinα)，其中λ，m，α为实数．若a＝2b，则的取值范围是(　)

A．[－6,1]　 　　　　　　　　　B．[4,8]

C．(－∞，1]　 　　　　　　　　D．[－1,6]

解析：选A.∵a＝2b.∴

消去λ，得4m²－8m+4－cos²α＝m+2sinα，

即4m²－9m+2＝－(sinα－1)².

∵－1≤sinα≤1，∴－4≤－(sinα－1)²≤0，

∴－4≤4m²－9m+2≤0，

解得≤m≤2，∴＝＝2－∈[－6,1]．

5．在△ABC中，已知D是AB边上一点，若＝2，＝+λ，则λ等于(　)

A. 　　　　　　　　　　　B.

C．－　 　　　　　　　　　D．－

解析：选A.法一：∵A、D、B三点共线，∴+λ＝1，

∴λ＝.故选A.

法二：∵＝2，∴＝，

∴＝+＝+＝+(－)

＝+＝+λ，

∴λ＝，故选A.

4．已知平面内有一点P及一个△ABC，若++＝，则(　)

A．点P在△ABC外部　 　　　　B．点P在线段AB上

C．点P在线段BC上　 　　　　D．点P在线段AC上

解析：选D.∵++＝，

∴++－＝0，

即+++＝0，

∴++＝0，

2＝，∴点P在线段AC上．