5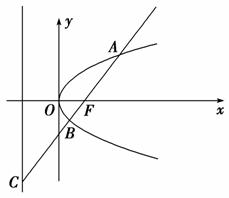．如图过抛物线y²＝2px(p＞0)的焦点F的直线依次交抛物线及准线于点A，B，C，若|BC|＝2|BF|，且|AF|＝3，则抛物线的方程为(　)

A．y²＝x

B．y²＝9x

C．y²＝x

D．y²＝3x

解析：选D.如图分别过点A，B作准线的垂线，分别交准线于点E，D，设|BF|＝a，则由已知得：|BC|＝2a，由定义得：|BD|＝a，故∠BCD＝30°，在直角三角形ACE中，|AE|＝3，|AC|＝3+3a，故有2|AE|＝|AC|⇒3+3a＝6，从而得a＝1，再由BD∥FG，则有＝⇒p＝，因此抛物线方程为y²＝3x.

4．抛物线y²＝4x的焦点为F，过F且倾斜角等于的直线与抛物线在x轴上方的曲线交于点A，则AF的长为(　)

A．2　 　　　　　　　　　B．4

C．6　 　　　　　　　　　D．8

解析：选B.由已知可得直线AF的方程为y＝(x－1)，联立直线与抛物线方程消元得：3x²－10x+3＝0，解之得：x₁＝3，x₂＝(据题意应舍去)，由抛物线定义可得：|AF|＝x_A+＝3+1＝4.

3．(2008年高考北京卷)若点P到直线x＝－1的距离比它到点(2,0)的距离小1，则点P的轨迹为(　)

A．圆 　　　　　　　　　　B．椭圆

C．双曲线　 　　　　　　　　D．抛物线

解析：选D.由题意知，点P到点(2,0)的距离与P到直线x＝－2的距离相等，由抛物线定义得点P的轨迹是以(2,0)为焦点，以直线x＝－2为准线的抛物线，故选D.

2．抛物线y＝4x²上的一点M到焦点的距离为1，则点M的纵坐标是(　)

A.　 　　　　　　　　　　B.

C.　 　　　　　　　　　　　D．0

解析：选B.M到焦点的距离为1，则其到准线距离也为1.

又∵抛物线的准线为y＝－，

∴M点的纵坐标为.

1．若抛物线y²＝2px的焦点与椭圆+＝1的右焦点重合，则p的值为(　)

A．－2　 　　　　　　　　　B．2

C．－4　 　　　　　　　　　D．4

解析：选D.抛物线的焦点为F(，0)，

椭圆中c²＝6－2＝4，

∴c＝2，其右焦点为(2,0)，

∴＝2，∴p＝4.

6．设抛物线y²＝2px(p＞0)的焦点为F，Q是抛物线上除顶点外的任意一点，直线QO交准线于P点，过Q且平行于抛物线对称轴的直线交准线于R点，求证：·＝0.

证明：设Q(，y₀)，则R(－，y₀)，

直线OQ的方程为y＝x，

将x＝－代入上式，得y＝－，

∴P(－，－)．又F(，0)，

∴＝(p，)，＝(p，－y₀)．

∴·＝0.

练习

5.设抛物线y²＝mx的准线与直线x＝1的距离为3，则抛物线的方程为________．

解析：当m＞0时，准线方程为x＝－＝－2，

∴m＝8，

此时抛物线方程为y²＝8x；

当m＜0时，准线方程为x＝－＝4，

∴m＝－16，

此时抛物线方程为y²＝－16x.

∴所求抛物线方程为y²＝8x或y²＝－16x.

答案：y²＝8x或y²＝－16x

4．过抛物线y²＝4x的焦点F作垂直于x轴的直线，交抛物线于A，B两点，则以F为圆心、AB为直径的圆的方程是________．

解析：由y²＝4x，得p＝2，F(1,0)，

∴A(1,2)，B(1，－2)，

∴所求圆的方程为(x－1)²+y²＝4.

答案：(x－1)²+y²＝4

3．(2009年高考山东卷)设斜率为2的直线l过抛物线y²＝ax(a≠0)的焦点F，且和y轴交于点A，若△OAF(O为坐标原点)的面积为4，则抛物线方程为(　)

A．y²＝±4x　 　　　　　B．y²＝±8x

C．y²＝4x　 　　　　　　D．y²＝8x

解析：选B.y²＝ax的焦点坐标为(，0)．过焦点且斜率为2的直线方程为y＝2(x－)，令x＝0得：y＝－.

∴×·＝4，∴a²＝64，∴a＝±8.

2．经过抛物线y²＝2x的焦点且平行于直线3x－2y+5＝0的直线的方程是(　)

A．6x－4y－3＝0　 　　　B．3x－2y－3＝0

C．2x+3y－2＝0　 　　　D．2x+3y－1＝0

解析：选A.据题意设所求平行直线方程为3x－2y+c＝0，又直线过抛物线y²＝2x的焦点(，0)，代入求得c＝－，故直线方程为6x－4y－3＝0.