1．(2010年滨州模拟)函数y＝(m－1)xm²－m为幂函数，则函数为(　)

A．奇函数 　　　　　　　B．偶函数

C．增函数　 　　　　　　　D．减函数

解析：选B.由题意知m＝2，则该函数为y＝x²，故选B.

12．已知P＝{x|x²－8x－20≤0}，S＝{x||x－1|≤m}．

(1)是否存在实数m，使x∈P是x∈S的充要条件，若存在，求出m的范围；

(2)是否存在实数m，使x∈P是x∈S的必要条件，若存在，求出m的范围．

解：(1)由题意x∈P是x∈S的充要条件，则P＝S.

由x²－8x－20≤0⇒－2≤x≤10，

∴P＝[－2,10]．

由|x－1|≤m⇒1－m≤x≤1+m，∴S＝[1－m,1+m]．

要使P＝S，则∴

∴这样的m不存在．

(2)由题意x∈P是x∈S的必要条件，则S⊆P.

由|x－1|≤m，可得1－m≤x≤m+1，

要使S⊆P，则∴m≤3.

综上，可知m≤3时，x∈P是x∈S的必要条件.

11．写出下殓命题的否命题及命题的否定形式，并判断其真假．

(1)m>0，则关于x的方程x²+x－m＝0有实数根．

(2)若x，y都是奇数，则x+y是奇数．

解：(1)否命题：若m≤0，则关于x的方程x²+x－m＝0无实数根，是假命题；命题的否定；若m>0，则关于x的方程x²+x－m＝0无实数根，假命题．

(2)否命题：若x、y不都是奇数，则x+y不是奇数，是假命题；

命题的否定：若x、y都是奇数，则x+y不是奇数，是真命题．

10．写出下列命题的逆命题、否命题、逆否命题，并判断其真假．

(1)实数的平方是非负数；

(2)等底等高的两个三角形是全等三角形．

(3)若ab＝0，则a＝0或b＝0；

解：(1)逆命题：若一个数的平方是非负数，则这个数是实数．真命题．

否命题：若一个数不是实数，则它的平方不是非负数．真命题．

逆否命题：若一个数的平方不是非负数，则这个数不是实数．真命题．

(2)逆命题：若两个三角形全等，则这两个三角形等底等高．真命题．

否命题：若两个三角形不等底或不等高，则这两个三角形不全等．真命题．

逆否命题：若两个三角形不全等，则这两个三角形不等底或不等高．假命题．

(3)逆命题：若a＝0或b＝0，则ab＝0.为真命题．

否命题：若ab≠0，则a≠0且b≠0.为真命题．

逆否命题：若a≠0且b≠0，则ab≠0.为真命题．

9．设计如图所示的四个电路图，条件A：“开关S₁闭合”；条件B：“灯泡L亮”，A是B的________条件．

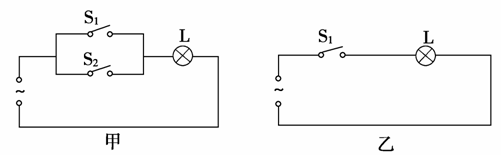
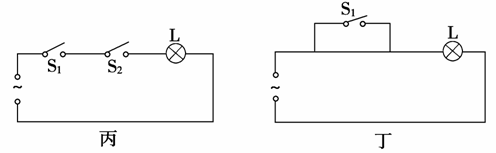
解析：对于图甲，A是B的充分不必要条件．对于图乙，A是B的充要条件．对于图丙，A是B的必要不充分条件．对于图丁，A是B的既不充分也不必要条件．

答案：充分不必要，充要，必要不充分，既不充分也不必要

8．设l₁、l₂表示两条直线，α表示平面，若有①l₁⊥l₂；②l₁⊥α；③l₂⊂α，则以其中两个为条件，另一个为结论，可以构造的所有命题中正确命题的个数为________．

解析：只有②③⇒①正确，故应填1.

答案：1

7．已知集合A＝{x|x>5}，集合B＝{x|x>a}，若命题“x∈A”是命题“x∈B”的充分不必要条件，则实数a的取值范围是________．

解析：由题意得，A是B的真子集，故a<5为所求．

答案：a<5

6．已知直线y＝2x上一点P的横坐标为a，有两个点A(－1,1)，B(3,3)，那么使向量与夹角为钝角的一个充分不必要条件是(　)

A．－1＜a＜2　 　　　　　　B．0＜a＜1

C．－＜a＜　 　　　　D．0＜a＜2

解析：选B.P(a,2a)，与夹角为钝角的充要条件是，解得0＜a＜1或1＜a＜2，故选B.

5．有下列四个命题：(1)“若xy＝1，则x，y互为倒数”的逆命题；(2)“面积相等的三角形全等”的否命题；(3)“若m≤1，则方程x²－2x+m＝0有实数解”的逆否命题；(4)“若A∩B＝A，则A⊆B”的逆否命题．其中真命题个数为(　)

A．1　 　　　　　　　　　　B．2

C．3　 　　　　　　　　　　D．4

解析：选D.(1)、(2)、(4)显然成立．(3)∵x²－2x+m＝0有实数解，∴Δ＝4－4m≥0，即m≤1.所以(3)成立．

4．(2009年高考北京卷)“α＝+2kπ(k∈Z)”是“cos2α＝”的(　)

A．充分而不必要条件 　　　B．必要而不充分条件

C．充分必要条件　 　　　　　D．既不充分也不必要条件

解析：选A.∵当α＝+2kπ(k∈Z)时，

cos2α＝cos(+4kπ)＝，

∴“α＝+2kπ(k∈Z)”是“cos2α＝”的充分条件．

而当α＝－时，cos2α＝，

但－≠+2kπ(k∈Z)，

∴“α＝+2kπ(k∈Z)”不是“cos2α＝”的必要条件．