2.(2010安徽文)(4)过点(1，0)且与直线x-2y-2=0平行的直线方程是

(A)x-2y-1=0　　　　 (B)x-2y+1=0　　　 (C)2x+y-2=0　　　　 (D)x+2y-1=0

[答案]A

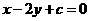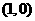[解析]设直线方程为，又经过，故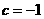，所求方程为.

[方法技巧]因为所求直线与与直线x-2y-2=0平行，所以设平行直线系方程为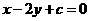，代入此直线所过的点的坐标，得参数值，进而得直线方程.也可以用验证法，判断四个选项中方程哪一个过点(1，0)且与直线x-2y-2=0平行.

1.(2010江西理)8.直线与圆相交于M,N两点，若，则k的取值范围是

A. 　　　　　B. 　C. 　　　　D.

[答案]A

[解析]考查直线与圆的位置关系、点到直线距离公式，重点考察数形结合的运用.

解法1：圆心的坐标为(3.，2)，且圆与y轴相切.当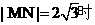，由点到直线距离公式，解得；

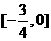解法2：数形结合，如图由垂径定理得夹在两直线之间即可， 不取，排除B，考虑区间不对称，排除C，利用斜率估值，选A

2010年高考题

4．若离散型随机变量的分布列为

则a等于________．

解析：由3a²+a+4a－1＝1求得．

3．(原创题)一盒中有12个乒乓球，其中9个新的，3个旧的，从盒子中任取3个球来用，用完后装回盒中，此时盒中旧球个数X是一个随机变量，其分布列为P(X)，则P(X＝4)的值为(　)

A.　　　　　　　　　 　B.

C. 　　　　　　　　　　D.

解析：选C.由题意取出的3个球必为2个旧球1个新球，故P(X＝4)＝＝.

2．(2010年海口市调研测试)设随机变量X等可能取值1,2,3，…，n，如果P(X＜4)＝0.3，那么(　)

A．n＝3 　　　　　　　　B．n＝4

C．n＝10　 　　　　　　　D．n＝9

解析：选C.∵P(X＝k)＝(k＝1,2,3，…，n)，

∴0.3＝P(X＜4)＝P(X＝1)+P(X＝2)+P(X＝3)＝.

∴n＝10.

1．某射手射击所得环数X的分布列为：

则此射手“射击一次命中环数大于7”的概率为(　)

A．0.28 　　　　　　　　　B．0.88

C．0.79 　　　　　　　　　D．0.51

解析：选C.P(X＞7)＝P(X＝8)+P(X＝9)+P(X＝10)＝0.28+0.29+0.22＝0.79.

8.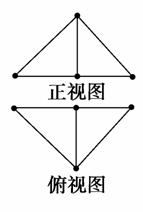(2010年温州模拟)把边长为1的正方形ABCD沿对角线BD折起，形成三棱锥C-ABD，其正视图与俯视图如图所示，则侧视图的面积为　　　.

解析：根据这两个视图可以推知折起后二面角C-BD-A为直角二面角，其侧视图是一个两直角边长为的直角三角形，其面积为.

7．如图所示为长方体木块堆成的几何体的三视图，此几何体共由__________块木块堆成．

解析：由三视图知，由4块木块组成．

答案：4

6．圆锥轴截面的顶角θ满足<θ<，则侧面展开图中中心角α满足(　)

A.<α< 　　　　　　　　　　　　B.<α<

C.<α<π 　　　　　　　　　　　　D．π<α<π

解析：选D.设圆锥母线长为R，底面圆的半径为r，

则r＝Rsin.又底面周长l＝2πr＝Rα，

即2πRsin＝Rα，∴α＝2πsin.

∵<θ<，∴<sin<，

∴π<α<π，故选D.