
题目列表(包括答案和解析)
5.(安徽省合肥市2009届高三上学期第一次教学质量检测)函数 在
在 上单调,则的取值范围是 ( )
上单调,则的取值范围是 ( )
A. B.
B.
C. D.
D.
答案 A
4.(2009广东三校一模)定义在 上的函数
上的函数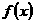 是奇函数又是以
是奇函数又是以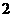 为周期的周期函数,则
为周期的周期函数,则
 等于 ( )
等于 ( )
A.-1 B.0 C.1 D.4
答案 B
3.(2009湘潭市一中12月考)已知定义在R上的函数 满足
满足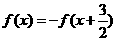 ,且
,且
 ,
, ,
, ( )
( )
A. B.
B. C.
C. D.
D.
答案 A
2.(2009龙岩一中)函数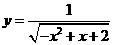 的定义域是 ( )
的定义域是 ( )
A.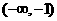 B.
B. C.
C. D.
D. 
答案 B
1. (北京市东城区2009年3月高中示范校高三质量检测文理)函数 的定义域是
的定义域是 ,若对于任意的正数
,若对于任意的正数 ,函数
,函数 都是其定义域上的增函数,则函数
都是其定义域上的增函数,则函数 的图象可能是 ( )
的图象可能是 ( )

答案 A
5、(2009南华一中12月月考)设函数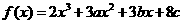 在
在 及
及 时取得极值.
时取得极值.
(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的 ,都有
,都有 成立,求c的取值范围.
成立,求c的取值范围.
解:(Ⅰ) ,
,
因为函数 在
在 及
及 取得极值,则有
取得极值,则有 ,
, .
.
即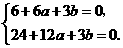 解得
解得 ,
,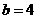 .………………………6分
.………………………6分
(Ⅱ)由(Ⅰ)可知,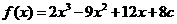 ,
,
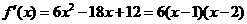 . ………………………7分
. ………………………7分
当 时,
时,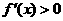 ;
;
当 时,
时, ;
;
当 时,
时,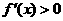 . ………………………8分
. ………………………8分
所以,当 时,
时, 取得极大值
取得极大值 ,又
,又 ,
,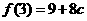 .
.
则当 时,
时, 的最大值为
的最大值为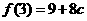 . ………………………10分
. ………………………10分
因为对于任意的 ,有
,有 恒成立,
恒成立,
所以 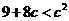 ,
,
解得  或
或 ,
,
因此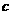 的取值范围为
的取值范围为 .………………………12分
.………………………12分
2009年联考题
4、(2009江门一模)已知函数 ,
, 是常数,
是常数, .
.
⑴若 是曲线
是曲线 的一条切线,求
的一条切线,求 的值;
的值;
⑵ ,试证明
,试证明 ,使
,使 .
.
⑴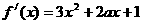 -------1分,解
-------1分,解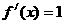 得,
得, 或
或 -------2分
-------2分
当 时,
时, ,
, ,所以
,所以 不成立-------3分
不成立-------3分
当 时,由
时,由 ,即
,即 ,得
,得 -----5分
-----5分
⑵作函数 -------6分
-------6分
 ,函数
,函数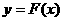 在
在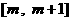 上的图象是一条连续不断的曲线------7分,
上的图象是一条连续不断的曲线------7分,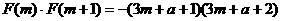 ------8分
------8分
①若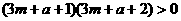 ,
, ,
, ,使
,使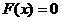 ,即
,即 -------10分
-------10分
②若 ,
, ,
, ,
,
 ,
, 当
当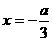 时有最小值
时有最小值 ,且当
,且当 时
时 -------11分,
-------11分,
所以存在 (或
(或 )从而
)从而 ,使
,使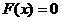 ,即
,即 -------12分
-------12分
3、(2009上海十校联考)已知函数 ,
, 有反函数,且函数
有反函数,且函数 的最大值为
的最大值为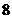 ,求实数
,求实数 的值.
的值.
解:因为函数有反函数,所以在定义域内是一一对应的
函数 的对称轴为
的对称轴为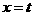 ,所以
,所以 或
或
若 ,在区间
,在区间 上函数是单调递增的,所以
上函数是单调递增的,所以 ,解得
,解得 ,符合
,符合
若 ,在区间
,在区间 上函数是单调递减的,所以
上函数是单调递减的,所以 ,解得
,解得 ,与
,与 矛盾,舍去
矛盾,舍去
综上所述,满足题意的实数 的值为
的值为
2、(2009滨州一模)设函数
(I)若直线l与函数 的图象都相切,且与函数
的图象都相切,且与函数 的图象相切于点
的图象相切于点
(1,0),求实数p的值;
(II)若 在其定义域内为单调函数,求实数p的取值范围;
在其定义域内为单调函数,求实数p的取值范围;
解:(Ⅰ)方法一:∵ ,
,
∴ .
.
设直线 ,
,
并设l与g(x)=x2相切于点M( )
)
∵
 ∴2
∴2
∴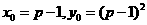
代入直线l方程解得p=1或p=3.
方法二:
将直线方程l代入 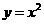 得
得

∴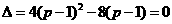
解得p=1或p=3 .
(Ⅱ)∵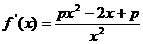 ,
,
①要使 为单调增函数,须
为单调增函数,须 在
在 恒成立,
恒成立,
即 在
在 恒成立,即
恒成立,即 在
在 恒成立,
恒成立,
又 ,所以当
,所以当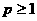 时,
时, 在
在 为单调增函数; ②要使
为单调增函数; ②要使 为单调减函数,须
为单调减函数,须 在
在 恒成立,
恒成立,
即 在
在 恒成立,即
恒成立,即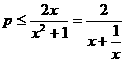 在
在 恒成立,
恒成立,
又 ,所以当
,所以当 时,
时, 在
在 为单调减函数.
为单调减函数.
综上,若 在
在 为单调函数,则
为单调函数,则 的取值范围为
的取值范围为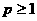 或
或 .
.
1、(2009上海八校联考)对定义在 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为 函数。
函数。
① 对任意的 ,总有
,总有 ;
;
② 当 时,总有
时,总有 成立。
成立。
已知函数 与
与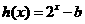 是定义在
是定义在 上的函数。
上的函数。
(1)试问函数 是否为
是否为 函数?并说明理由;
函数?并说明理由;
(2)若函数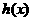 是
是 函数,求实数
函数,求实数 组成的集合;
组成的集合;
解:(1)当 时,总有
时,总有 ,满足①,
,满足①,
当 时,
时,
 ,满足②
,满足②
(2) 为增函数,
为增函数,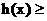


由 ,得
,得 ,
,
即
因为 
所以 

 与
与 不同时等于1
不同时等于1
 ;
; 
当 时,
时, ;
; 
综合上述:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com