
题目列表(包括答案和解析)
6.(2010浙江文)(13)已知平面向量 则
则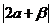 的值是
的值是
答案 :
5.(2010浙江文)(17)在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点,在APMC中任取一点记为E,在B、Q、N、D中任取一点记为F,设G为满足向量 的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为
。
的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为
。

答案:
4. (2010江西理)13.已知向量
(2010江西理)13.已知向量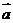 ,
, 满足
满足 ,
, ,
, 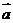 与
与 的夹角为60°,则
的夹角为60°,则
[答案] 
[解析]考查向量的夹角和向量的模长公式,以及向量三角形法则、余弦定理等知识,如图 ,由余弦定理得:
,由余弦定理得:
3.(2010陕西文)12.已知向量a=(2,-1),b=(-1,m),c=(-1,2)若(a+b)∥c,则
m= .
[答案]-1
解析: ,所以m=-1
,所以m=-1
2.(2010浙江理)(16)已知平面向量 满足
满足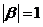 ,且
,且 与
与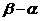 的夹角为120°,则
的夹角为120°,则 的取值范围是__________________ .
的取值范围是__________________ .
解析:利用题设条件及其几何意义表示在三角形中,即可迎刃而解,本题主要考察了平面向量的四则运算及其几何意义,突出考察了对问题的转化能力和数形结合的能力,属中档题。
1.(2010上海文)13.在平面直角坐标系中,双曲线 的中心在原点,它的一个焦点坐标为
的中心在原点,它的一个焦点坐标为 ,
, 、
、 分别是两条渐近线的方向向量。任取双曲线
分别是两条渐近线的方向向量。任取双曲线 上的点
上的点 ,若
,若 (
(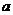 、
、 ),则
),则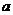 、
、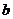 满足的一个等式是 4ab=1
。
满足的一个等式是 4ab=1
。
解析:因为 、
、 是渐进线方向向量,所以双曲线渐近线方程为
是渐进线方向向量,所以双曲线渐近线方程为 ,又
,又
双曲线方程为 ,
, =
= ,
,
 ,化简得4ab=1
,化简得4ab=1
20.(2010湖北理)5.已知 和点M满足
和点M满足 .若存在实数m使得
.若存在实数m使得 成立,则m=
成立,则m=
A.2 B.3 C.4 D.5

19.(2010年安徽理)

18.(2010湖南理)4、在 中,
中, =90°AC=4,则
=90°AC=4,则 等于
等于
A、-16 B、-8 C、8 D、16

17.(2010山东理)(12)定义平面向量之间的一种运算“ ”如下,对任意的
”如下,对任意的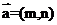 ,
,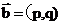 ,令
,令 ,下面说法错误的是( )
,下面说法错误的是( )
A.若 与
与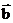 共线,则
共线,则 B.
B.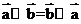
C.对任意的 ,有
,有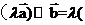
 D.
D. 
[答案]B
[解析]若 与
与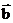 共线,则有
共线,则有 ,故A正确;因为
,故A正确;因为 ,而
,而
 ,所以有
,所以有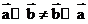 ,故选项B错误,故选B。
,故选项B错误,故选B。
[命题意图]本题在平面向量的基础上,加以创新,属创新题型,考查平面向量的基础知识以及分析问题、解决问题的能力。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com