
题目列表(包括答案和解析)
7.(2009北京卷理)已知向量a、b不共线,c a
a b
b R),d
R),d a
a b,如果c
b,如果c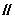 d,那么
( )
d,那么
( )
A. 且c与d同向
B.
且c与d同向
B. 且c与d反向
且c与d反向
C. 且c与d同向
D.
且c与d同向
D. 且c与d反向
且c与d反向
答案 D
解析 本题主要考查向量的共线(平行)、向量的加减法. 属于基础知识、基本运算的考
查.
取a ,b
,b ,若
,若 ,则c
,则c a
a b
b ,d
,d a
a b
b ,
,
显然,a与b不平行,排除A、B.
若 ,则c
,则c
 a
a b
b ,d
,d
 a
a b
b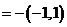 ,
,
即c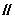 d且c与d反向,排除C,故选D.
d且c与d反向,排除C,故选D.
5.(2009北京卷文)已知向量 ,如果
,如果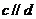
那么 ( )
A. 且
且 与
与 同向
B.
同向
B. 且
且 与
与 反向
反向
C. 且
且 与
与 同向
D.
同向
D. 且
且 与
与 反向
反向
答案 D
.w解析 本题主要考查向量的共线(平行)、向量的加减法. 属于基础知识、基本运算考查.
∵a ,b
,b ,若
,若 ,则c
,则c a
a b
b ,d
,d a
a b
b ,
,
显然,a与b不平行,排除A、B.
若 ,则c
,则c
 a
a b
b ,d
,d
 a
a b
b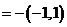 ,
,
即c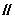 d且c与d反向,排除C,故选D.
d且c与d反向,排除C,故选D.
4.(2009浙江卷文)已知向量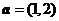 ,
, .若向量
.若向量 满足
满足 ,
, ,则
,则
 ( )
( )
A. B.
B.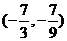 C.
C. D.
D.
答案 D
解析 不妨设 ,则
,则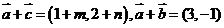 ,对于
,对于 ,则有
,则有 ;又
;又 ,则有
,则有 ,则有
,则有
[命题意图]此题主要考查了平面向量的坐标运算,通过平面向量的平行和垂直关系的考查,很好地体现了平面向量的坐标运算在解决具体问题中的应用.
3.(2009浙江卷理)设向量 ,
,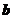 满足:
满足: ,
, ,
, .以
.以 ,
,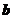 ,
, 的模为边长构成三角形,则它的边与半径为
的模为边长构成三角形,则它的边与半径为 的圆的公共点个数最多为
( ) w
的圆的公共点个数最多为
( ) w
A.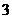 B.4 C.
B.4 C.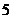 D.
D.
答案 C
解析 对于半径为1的圆有一个位置是正好是三角形的内切圆,此时只有三个交点,
对于圆的位置稍一右移或其他的变化,能实现4个交点的情况,但5个以上的交点不能
实现.
2.(2009广东卷理)一质点受到平面上的三个力 (单位:牛顿)的作用而处于平衡状态.已知
(单位:牛顿)的作用而处于平衡状态.已知 ,
, 成
成 角,且
角,且 ,
, 的大小分别为2和4,则
的大小分别为2和4,则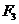 的大小为( ) A. 6 B. 2 C.
的大小为( ) A. 6 B. 2 C. 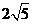 D.
D. 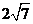
答案 D
解析  ,所以
,所以 ,选D.
,选D.
1.(2009年广东卷文)已知平面向量a=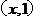 ,b=
,b= ,
则向量
,
则向量 ( )
( )
A平行于 轴
B.平行于第一、三象限的角平分线
轴
B.平行于第一、三象限的角平分线
C.平行于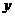 轴 D.平行于第二、四象限的角平分线
轴 D.平行于第二、四象限的角平分线
答案 C
解析 
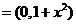 ,由
,由 及向量的性质可知,C正确.
及向量的性质可知,C正确.
1.(2010江苏卷)15、(本小题满分14分)
在平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C(-2,-1)。
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长;
(2)设实数t满足( )·
)·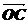 =0,求t的值。
=0,求t的值。
[解析]本小题考查平面向量的几何意义、线性运算、数量积,考查运算求解能力。满分14分。
(1)(方法一)由题设知 ,则
,则

所以
故所求的两条对角线的长分别为 、
、 。
。
(方法二)设该平行四边形的第四个顶点为D,两条对角线的交点为E,则:
E为B、C的中点,E(0,1)
又E(0,1)为A、D的中点,所以D(1,4)
故所求的两条对角线的长分别为BC= 、AD=
、AD= ;
;
(2)由题设知: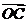 =(-2,-1),
=(-2,-1),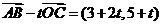 。
。
由( )·
)·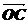 =0,得:
=0,得: ,
,
从而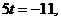 所以
所以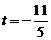 。
。
或者: ,
,

2009年高考题
8.(2010广东理)10.若向量 =(1,1,x),
=(1,1,x),  =(1,2,1),
=(1,2,1),  =(1,1,1),满足条件
=(1,1,1),满足条件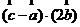 =-2,则
=-2,则 = .
= .
[答案]2
 ,
,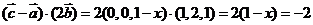 ,解得
,解得 .
.
7.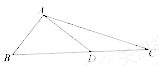 (2010天津理)(15)如图,在
(2010天津理)(15)如图,在 中,
中, ,
, ,
,
 ,则
,则 .
.
[答案]D
[解析]本题主要考查平面向量的基本运算与解三角形的基础知识,属于难题。
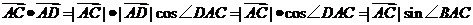

[解析]近几年天津卷中总可以看到平面向量的身影,且均属于中等题或难题,应加强平面向量的基本运算的训练,尤其是与三角形综合的问题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com