
题目列表(包括答案和解析)
2010年高考题
5. 在△ABC中,角A、B、C的对边分别为a、b、c,若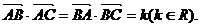
(Ⅰ)判断△ABC的形状; (Ⅱ)若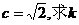 的值.
的值.
解:(I)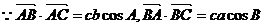
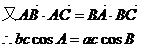
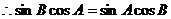
即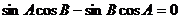
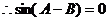
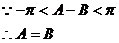
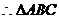 为等腰三角形.
为等腰三角形.
(II) 由(I)知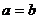
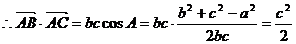
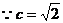
4.(2008年成都名校联盟高考数学冲刺预测卷二)在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2a-c)cosB=bcosC.
(Ⅰ)求角B的大小;
|
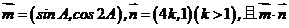 的最大值是5,求k的值.
的最大值是5,求k的值.
解:(I)∵(2a-c)cosB=bcosC,
∴(2sinA-sinC)cosB=sinBcosC
即2sinAcosB=sinBcosC+sinCcosB
=sin(B+C)
∵A+B+C=π,∴2sinAcosB=sinA
∵0<A<π,∴sinA≠0.
∴cosB=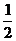
∵0<B<π,∴B=
(II)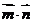 =4ksinA+cos2A
=4ksinA+cos2A
=-2sin2A+4ksinA+1,A∈(0,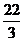 )
)
设sinA=t,则t∈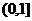 .
.
则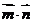 =-2t2+4kt+1=-2(t-k)2+1+2k2,t∈
=-2t2+4kt+1=-2(t-k)2+1+2k2,t∈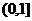
∵k>1,∴t=1时,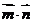 取最大值.
取最大值.
依题意得,-2+4k+1=5,∴k=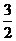
3.(江苏省滨海县08届高三第三次联考数学试卷)在 中,
中,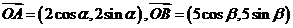 ,若
,若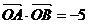 ,
则
,
则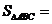 .
.
答案 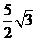
2.(2007届高三数学二轮复习新型题专题训练)已知 中
,角A,B,C的对边分别为a,b,c,AH为BC边上有高,以下结论:①
中
,角A,B,C的对边分别为a,b,c,AH为BC边上有高,以下结论:①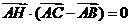 ;②
;②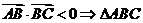 为锐角三角形③
为锐角三角形③
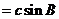 ;④
;④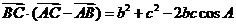 ,其中正确的个数是
,其中正确的个数是
A.1 B.2 C.3 D.4
答案 B
1.(2008东北师大附中模拟)在△ABC中,若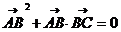 ,则△
,则△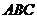 的形状为 ( )
的形状为 ( )
A.等腰三角形 B.等边三角形 C.等腰直角三角形 D.直角三角形
答案 D
18.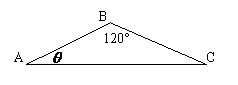 (2009广东省清远一中高三综合测试)已知
(2009广东省清远一中高三综合测试)已知 中,
中,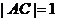 ,
, ,
,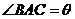 ,记
,记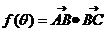 ,
,
(1)求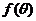 关于
关于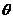 的表达式;
的表达式;
(2)求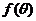 的值域;
的值域;
解(1)由正弦定理有: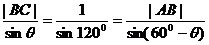 ;
;
∴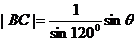 ,
,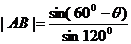 ;
;
∴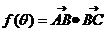
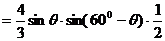
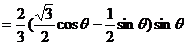
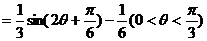
(2)由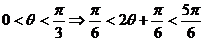 ;
;
∴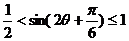 ;∴
;∴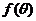
2007-2008年联考题
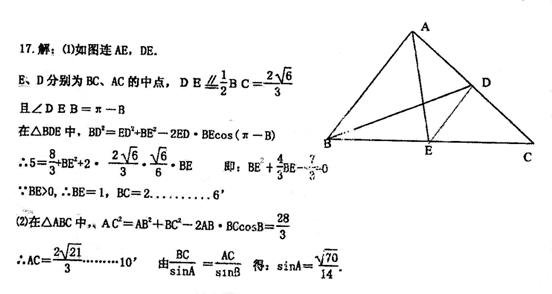
17.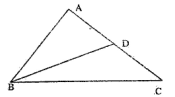 (天津市河东区2009年高三一模)如图所示,在△ABC,已知
(天津市河东区2009年高三一模)如图所示,在△ABC,已知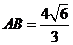 ,
,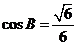 ,AC边上的中线
,AC边上的中线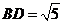 ,
,
求:(1)BC的长度;
(2) 的值。
的值。
16.(福建省泉州一中2009年高三模拟)在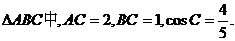
(1)求边AB的长;
(2)求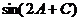 的值。
的值。
解:(1)由余弦定理,得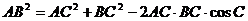
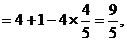
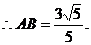
(2)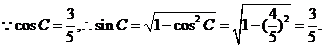
由正弦定理,得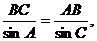
即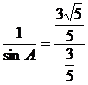 ,
,
解得
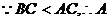 为锐角,
为锐角,
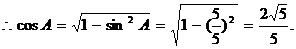
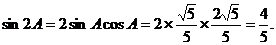
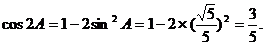
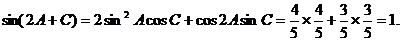
15.(安徽省合肥市一六八中学2009届高三适应性训练) 在 中,
中,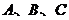 的对边
的对边
分别是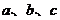 ,且满足
,且满足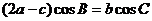 .(1)求
.(1)求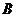 的大小;
(2)设m
的大小;
(2)设m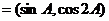 ,n
,n
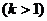 ,且m·n的最大值是5,求
,且m·n的最大值是5,求 的值.
的值.
解(1)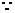
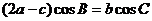 ,
,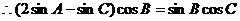 ,
,
即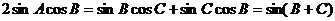
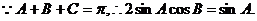
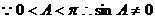 .
. 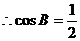 .
.

(2)m·n= ,
,
设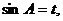 则
则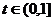 .
.
则m·n=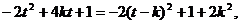
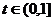
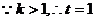 时,m·n取最大值.
时,m·n取最大值.
依题意得,(m·n) =
=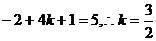
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com