
题目列表(包括答案和解析)
52、(2009扬州大学附中3月月考)设 是把坐标平面上的点的横坐标伸长到
是把坐标平面上的点的横坐标伸长到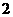 倍,纵坐
倍,纵坐
标伸长到 倍的伸压变换.(Ⅰ)求矩阵
倍的伸压变换.(Ⅰ)求矩阵 的特征值及相应的特征向量;
的特征值及相应的特征向量;
(Ⅱ)求逆矩阵 以及椭圆
以及椭圆 在
在 的作用下的新曲线的方程.
的作用下的新曲线的方程.
解(Ⅰ)由条件得矩阵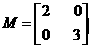 ,
,
它的特征值为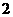 和
和 ,对应的特征向量为
,对应的特征向量为 及
及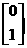 ;
;
(Ⅱ)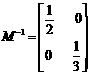 ,椭圆
,椭圆 在
在 的作用下的新曲线的方程为
的作用下的新曲线的方程为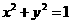 .
.
51、(2009通州第四次调研)(不等式选讲)对于任意实数a(a≠0)和b,不等式|a+b|+|a-b|≥|a|(|x-1|+|x-2|恒成立,试求实数x的取值范围.
解 由题知,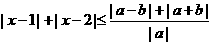 恒成立,故|x-1|+|x-2|不大于
恒成立,故|x-1|+|x-2|不大于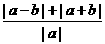 的最小值
的最小值
∵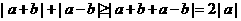 当且仅当(a+b)(a-b) ≥0时取等号
当且仅当(a+b)(a-b) ≥0时取等号
∴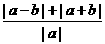 的最小值等于2.
5分
的最小值等于2.
5分
∴x的范围即为不等式|x-1|+|x-2|≤2的解
解不等式得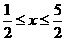 10分
10分
50、(2009通州第四次调研)(矩阵与变换)已知矩阵
 ,向量
,向量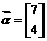 .
.
(1)求矩阵 的特征值
的特征值 、
、 和特征向量
和特征向量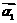 、
、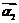 ;
;
(2)求 的值.
的值.
解 (1)矩阵 的特征多项式为
的特征多项式为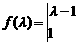
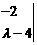
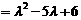 ,
,
令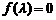 ,得
,得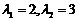 ,
,
当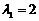 时,得
时,得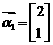 ,当
,当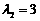 时,得
时,得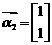 .
…………………5分
.
…………………5分
(2)由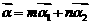 得
得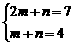 ,得
,得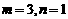 .
.
∴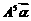
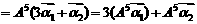
 .……………………10分
.……………………10分
49、(2009南京一模)选修4-5:不等式选讲,已知 为正数,求证:
为正数,求证: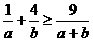 .
.
证明: ,所以
,所以 
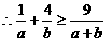
48、(2009金陵中学三模)(1)设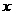 是正数,求证:
是正数,求证: ;
;
(2)若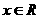 ,不等式
,不等式 是否仍然成立?如果仍成立,请给出证明;如果不成立,请举出一个使它不成立的
是否仍然成立?如果仍成立,请给出证明;如果不成立,请举出一个使它不成立的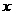 的值.
的值.
简证:(1)∵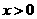 ,∴
,∴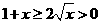 ,
,
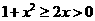 ,
,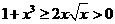 ,三个
,三个
同向正值不等式相乘得 . ---------5分
. ---------5分
简解:(2)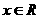 时原不等式仍然成立.
时原不等式仍然成立.
思路1:分类讨论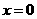 、
、 、
、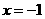 、
、 证;
证;
思路2:左边= .---------------10分
.---------------10分
47、(2009南京一模)已知矩阵 ,
, 。在平面直角坐标系中,设直线
。在平面直角坐标系中,设直线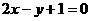 在矩阵
在矩阵 对应的变换作用下得到的曲线
对应的变换作用下得到的曲线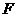 ,求曲线
,求曲线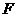 的方程
的方程
解 由题设得 ,设
,设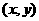 是直线
是直线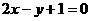 上任意一点,
上任意一点,
点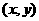 在矩阵
在矩阵 对应的变换作用下变为
对应的变换作用下变为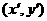 ,
,
则有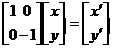 , 即
, 即 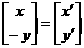 ,所以
,所以
因为点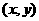 在直线
在直线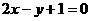 上,从而
上,从而 ,即:
,即: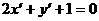
所以曲线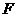 的方程为
的方程为 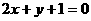
46、(2009厦门英才学校)(极坐标与参数方程)求极坐标系中,圆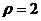 上的点到直线
上的点到直线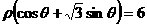 的距离的最小值.
的距离的最小值.
解 由 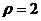 即
即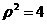 则易得
则易得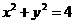 ,由
,由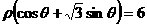 易得
易得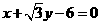
 圆心
圆心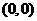 到直线的距离为
到直线的距离为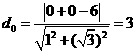
 又圆的半径为2 ,
又圆的半径为2 ,  圆上的点到直线的距离的最小值为
圆上的点到直线的距离的最小值为 .
.
45、(2009厦门十中)(极坐标与参数方程)已知圆C的参数方程为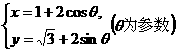 ,若P是圆C与x轴正半轴的交点,以原点O为极点,x轴的正半轴为极轴建立极坐标系,设过点P的圆C的切线为l,求直线l的极坐标方程.
,若P是圆C与x轴正半轴的交点,以原点O为极点,x轴的正半轴为极轴建立极坐标系,设过点P的圆C的切线为l,求直线l的极坐标方程.
解 由题设知,圆心

∠CPO=60°,故过P点的切线飞倾斜角为30°
设 ,是过P点的圆C的切线上的任一点,则在△PMO中,
,是过P点的圆C的切线上的任一点,则在△PMO中,
∠MOP=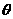

由正弦定理得
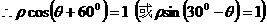 ,即为所求切线的极坐标方程。
,即为所求切线的极坐标方程。
44、(2009厦门乐安中学)(极坐标与参数方程)在极坐标系中,设圆 上的点到直线
上的点到直线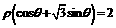 的距离为
的距离为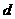 ,求
,求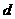 的最大值.
的最大值.
解 将极坐标方程 转化为普通方程:
转化为普通方程:
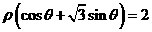 可化为
可化为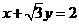
在 上任取一点A
上任取一点A ,则点A到直线的距离为
,则点A到直线的距离为
 ,它的最大值为4
,它的最大值为4
43、(2009厦门集美中学)(极坐标与参数方程)求曲线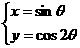 过点
过点 的切线方程.
的切线方程.
 ,消去参数
,消去参数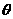 得
得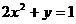 .
.
设切线为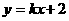 ,代入得
,代入得
令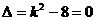 ,得
,得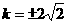 ,故
,故 即为所求.
即为所求.
或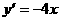 ,设切点为
,设切点为 ,则斜率为
,则斜率为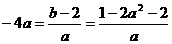 ,解得
,解得 ,
,
即得切线方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com