
题目列表(包括答案和解析)
3、(2009昆明市期末理)设集合A={0,2,4}、B={1,3,5}。分别从A、B中任取2个元素组成无重复数字的四位数,其中不能被5整除的数共有 ( )
A.64个 B 104个
C.116个 D.152个
答案 C
2、(2009金华一中2月月考) 将4名新来的同学分配到A、B、C三个班级中,每个班级至少安排1名学生,其中甲同学不能分配到A班,那么不同的分配方案有 ( )
A. 18种 B. 24种 C. 54种 D. 60种
答案 B
1、(2009聊城一模)2008年北京奥运会期间,计划将5名志愿者分配到3个不同的奥运场
馆参加接待工作,每个场馆至少分配一名志愿者的方案种数为 ( )
A.540 B.300 C.150 D.180
答案 C
9.(肥城市第二次联考)已知杨辉三角
1
1 1
1 2 1
1 3 3 1
…………………………
① 将第4行的第1个数乘以1, 第2个数乘以2, 第3个数乘以4, 第4个数乘以8后,这一行所有数字之和等于 (用数字作答);
② 若等比数列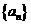 的首项是
的首项是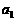 ,公比是
,公比是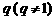 ,将杨辉三角的第
,将杨辉三角的第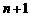 行的第1个数乘以
行的第1个数乘以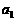 ,第2个数乘以
,第2个数乘以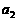 ,……,第
,……,第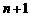 个数乘以
个数乘以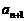 后,这一行的所有数字之和等于 (用
后,这一行的所有数字之和等于 (用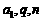 表示)
表示)
答案: 27,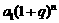
8. (玉溪一中期中)如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,且两端的格子的颜色也不同,则不同的涂色方法共有 种(用数字作答).
(玉溪一中期中)如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,且两端的格子的颜色也不同,则不同的涂色方法共有 种(用数字作答).
答案:630
7.(玉溪一中期中).若二项式(x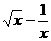 )
)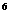 展开式中的第5项是5,则x等于_________.
展开式中的第5项是5,则x等于_________.
答案:3
6.(昆明一中一次月考理)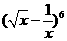 的展开式中,常数项为
.(用数字作答)
的展开式中,常数项为
.(用数字作答)
答案;4
5.(昆明一中三次月考理)将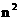 个正整数
个正整数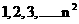 填入
填入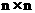 个方格中,使得每列、每条对角线上的数的和相等,这个正方形就叫做n阶幻方.如右图,就是一个3阶幻方,定义
个方格中,使得每列、每条对角线上的数的和相等,这个正方形就叫做n阶幻方.如右图,就是一个3阶幻方,定义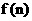 为n阶幻方对角线上数的和,例如
为n阶幻方对角线上数的和,例如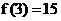 ,那么
,那么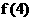 =
=
答案: =34
=34
4.(2009玉溪一中期中)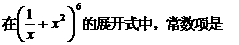 .
.
答案 15
3.(2009牟定一中期中)若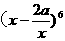 的展开式中常数项为
的展开式中常数项为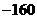 ,则展开式中各项系数之和为_
__.
,则展开式中各项系数之和为_
__.
答案 1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com