
题目列表(包括答案和解析)
2.(2010湖南文)11.在区间[-1,2]上随即取一个数x,则x∈[0,1]的概率为 。
[答案]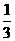
[命题意图]本题考察几何概率,属容易题。
1.(2010上海文)10. 从一副混合后的扑克牌(52张)中随机抽取2张,则“抽出的2张
均为红桃”的概率为 (结果用最简分数表示)。
[答案]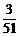
解析:考查等可能事件概率“抽出的2张均为红桃”的概率为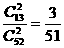
6.(2010湖北理)4.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件A,“骰子向上的点数是3”为事件B,则事件A,B中至少有一件发生的概率是
A  B
B 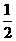 C
C 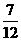 D
D 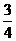

5.(2010广东理)8.为了迎接2010年广州亚运会,某大楼安装5个彩灯,它们闪亮的顺序不固定,每个彩灯彩灯闪亮只能是红、橙、黄、绿、蓝中的一种颜色,且这5个彩灯所闪亮的颜色各不相同.记这5个彩灯有序地闪亮一次为一个闪烁,在每个闪烁中,每秒钟有且仅有一个彩灯闪亮,而相邻两个闪烁的时间间隔均为5秒。如果要实现所有不同的闪烁,那么需要的时间至少是( )
A、 1205秒 B.1200秒 C.1195秒 D.1190秒
[答案]C
每次闪烁时间5秒,共5×120=600s,每两次闪烁之间的间隔为5s,共5×(120-1)=595s.总共就有600+595=1195s.
4.(2010北京文)⑶从{1,2,3,4,5}中随机选取一个数为a,从{1,2,3}中随机选取一个数为b,则b>a的概率是
(A)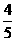 (B)
(B)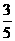 (C)
(C)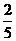 (D)
(D)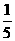
[答案]D
3.(2010安徽文)(10)甲从正方形四个顶点中任意选择两个顶点连成直线,乙从该正方形四个顶点中任意选择两个顶点连成直线,则所得的两条直线相互垂直的概率是
(A)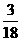 (A)
(A)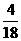 (A)
(A) (A)
(A)
[答案]C
[解析]正方形四个顶点可以确定6条直线,甲乙各自任选一条共有36个基本事件。两条直线相互垂直的情况有5种(4组邻边和对角线)包括10个基本事件,所以概率等于.
[方法技巧]对于几何中的概率问题,关键是正确作出几何图形,分类得出基本事件数,然后得所求事件保护的基本事件数,进而利用概率公式求概率.
2.(2010江西理)11.一位国王的铸币大臣在每箱100枚的硬币中各掺入了一枚劣币,国王怀疑大臣作弊,他用两种方法来检测。方法一:在10箱子中各任意抽查一枚;方法二:在5箱中各任意抽查两枚。国王用方法一、二能发现至少一枚劣币的概率分别为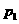 和
和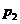 ,则
,则
A. 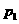 =
=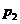 B.
B. 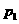 <
<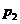 C.
C. 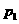 >
>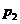 D。以上三种情况都有可能
D。以上三种情况都有可能
[答案]B
[解析]考查不放回的抽球、重点考查二项分布的概率。本题是北师大版新课标的课堂作业,作为旧大纲的最后一年高考,本题给出一个强烈的导向信号。方法一:每箱的选中的概率为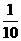
,总概率为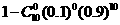 ;同理,方法二:每箱的选中的概率为
;同理,方法二:每箱的选中的概率为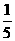 ,总事件的概率为
,总事件的概率为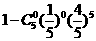 ,作差得
,作差得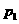 <
<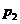 。
。
1.(2010辽宁理)(3)两个实习生每人加工一个零件.加工为一等品的概率分别为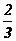 和
和 ,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为
,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为
(A)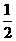 (B)
(B)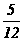 (C)
(C)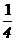 (D)
(D)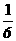
[答案]B
[命题立意]本题考查了相互独立事件同时发生的概率,考查了有关概率的计算问题
[解析]记两个零件中恰好有一个一等品的事件为A,则
P(A)=P(A1)+ P(A2)=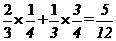
2010年高考题
7、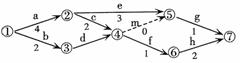 (2008上海市浦东新区第一学期期末质量抽测)
(2008上海市浦东新区第一学期期末质量抽测)
某工程的工序流程如图所示. 若该工程总时数
为9天,则工序d的天数x最大为__________.
答案 4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com