
题目列表(包括答案和解析)
6.(2010山东理)(8)某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在第四位、节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有
(A)36种 (B)42种 (C)48种 (D)54种
[答案]B

5.(2010四川文)(4)一个单位有职工800人,期中具有高级职称的160人,具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是
(A)12,24,15,9 (B)9,12,12,7 (C)8,15,12,5 (D)8,16,10,6
解析:因为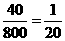
故各层中依次抽取的人数分别是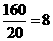 ,
,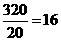 ,
,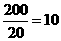 ,
,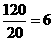
答案:D
7.B. =0.3413,
=0.3413,
 =0.5-0.3413=0.1587.
=0.5-0.3413=0.1587.
4.(2010广东理)7.已知随机变量X服从正态分布N(3.1),且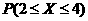 =0.6826,则p(X>4)=( )
=0.6826,则p(X>4)=( )
A、0.1588 B、0.1587 C、0.1586 D0.1585
3.(2010山东文)(6)在某项体育比赛中,七位裁判为一选手打出的分数如下:
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为
(A)92 , 2 (B) 92 , 2.8
(C) 93 , 2 (D) 93 , 2.8
答案:B
2.(2010重庆文)(5)某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本 . 若样本中的青年职工为7人,则样本容量为
(A)7 (B)15 (C)25 (D)35
[答案] B
解析:青年职工、中年职工、老年职工三层之比为7:5:3,所以样本容量为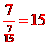
1.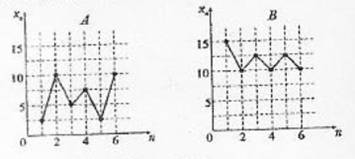 (2010陕西文)4.如图,样本A和B分别取自两个不同的总体,它们的样本平均数分别为
(2010陕西文)4.如图,样本A和B分别取自两个不同的总体,它们的样本平均数分别为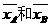 ,样本标准差分别为sA和sB,则 [B]
,样本标准差分别为sA和sB,则 [B]
(A) 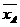 >
>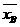 ,sA>sB
,sA>sB
(B) 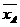 <
<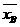 ,sA>sB
,sA>sB
(C) 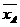 >
>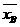 ,sA<sB
,sA<sB
(D) 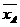 <
<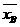 ,sA<sB
,sA<sB
解析:本题考查样本分析中两个特征数的作用
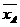 <10<
<10<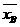 ;A的取值波动程度显然大于B,所以sA>sB
;A的取值波动程度显然大于B,所以sA>sB
2010年高考题
2.(2010全国卷2理)(20)(本小题满分12分)
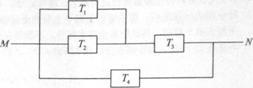
如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是p,电流能通过T4的概率是0.9.电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999.
(Ⅰ)求p;
(Ⅱ)求电流能在M与N之间通过的概率;
(Ⅲ)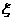 表示T1,T2,T3,T4中能通过电流的元件个数,求
表示T1,T2,T3,T4中能通过电流的元件个数,求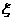 的期望.
的期望.
[命题意图]本试题主要考查独立事件的概率、对立事件的概率、互斥事件的概率及数学期望,考查分类讨论的思想方法及考生分析问题、解决问题的能力.
1.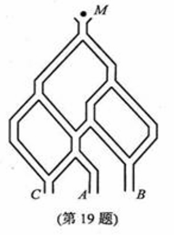 (2010浙江理)19.(本题满分l4分)如图,一个小球从M处投入,通过管道自上而下落A或B或C。已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.
(2010浙江理)19.(本题满分l4分)如图,一个小球从M处投入,通过管道自上而下落A或B或C。已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.
(I)已知获得l,2,3等奖的折扣率分别为50%,70%,90%.记随变量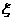 为获得k(k=1,2,3)等奖的折扣率,求随机变量
为获得k(k=1,2,3)等奖的折扣率,求随机变量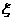 的分布列及期望
的分布列及期望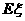 ;
;
(II)若有3人次(投入l球为l人次)参加促销活动,记随机变量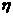 为获得1等奖或2等奖的人次,求
为获得1等奖或2等奖的人次,求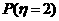 .
.
解析:本题主要考察随机事件的概率和随机变量的分布列、数学期望、二项分布等概念,同时考查抽象概括、运算求解能力和应用意识。
(Ⅰ)解:由题意得ξ的分布列为
|
ξ |
50% |
70% |
90% |
|
p |
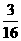 |
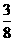 |
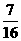 |
则Εξ=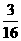 ×50%+
×50%+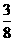 ×70%+
×70%+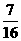 90%=
90%=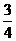 .
.
(Ⅱ)解:由(Ⅰ)可知,获得1等奖或2等奖的概率为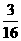 +
+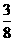 =
=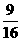 .
.
由题意得η-(3,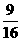 )
)
则P(η=2)=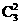 (
(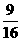 )2(1-
)2(1-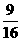 )=
)=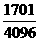 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com