
题目列表(包括答案和解析)
23.(2009天津卷文)(本小题满分12分)为了了解某工厂开展群众体育活动的情况,拟采
用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)求从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,用列举法计算这2个
工厂中至少有1个来自A区的概率。
解 (1)工厂总数为18+27+18=63,样本容量与总体中的个体数比为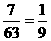 ,所以从
,所以从
A,B,C三个区中应分别抽取的工厂个数为2,3,2.
(2)设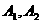 为在A区中抽得的2个工厂,
为在A区中抽得的2个工厂,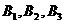 为在B区中抽得的3个工厂,
为在B区中抽得的3个工厂,
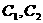 为在C区中抽得的2个工厂,这7个工厂中随机的抽取2个,全部的可能结果
为在C区中抽得的2个工厂,这7个工厂中随机的抽取2个,全部的可能结果
有: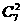 种,随机的抽取的2个工厂至少有一个来自A区的结果有
种,随机的抽取的2个工厂至少有一个来自A区的结果有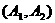 ,
,
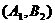
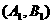
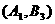
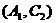
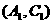 ,同理
,同理 还能组合5种,一共有11种.
还能组合5种,一共有11种.
所以所求的概率为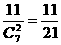
[考点定位]本小题主要考查分层抽样、用列举法计算随机事件所含的基本事件数及事
件发生的概率等基础知识,考查运用统计、概率知识解决实际问题的能力。
22.(2009安徽卷文)(本小题满分12分)某良种培育基地正在培育一种小麦新品种A,将
其与原有的一个优良品种B进行对照试验,两种小麦各种植了25亩,所得亩产数据(单
位:千克)如下:
品种A:357,359,367,368,375,388,392,399,400,405,414,
415,421,423,423,427,430,430,434,443,445,451,454
品种B:363,371,374,383,385,386,391,392,394,395,397
397,400,401,401,403,406,407,410,412,415,416,422,430
(Ⅰ)完成所附的茎叶图
(Ⅱ)用茎叶图处理现有的数据,有什么优点?
(Ⅲ)通过观察茎叶图,对品种A与B的亩产量及其稳定性进行比较,写出统计结论。
思路 由统计知识可求出A、B两种品种的小麦稳定性大小并画出茎叶图,用茎叶图处理数据,看其分布就比较明了。
解析 (1)茎叶图如图所示
|
A |
|
B |
|
9 7 |
35 |
|
|
8 7 |
36 |
3 |
|
5 |
37 |
1 4 |
|
8 |
38 |
3 5 6 |
|
9 2 |
39 |
1 2 4 457 7 |
|
5 0 |
40 |
0 1 1 3 6 7 |
|
5 4 2 |
41 |
0 2 5 6 |
|
7 3 3 1 |
42 |
2 |
|
4 0 0 |
43 |
0 |
|
5 5 3 |
44 |
|
|
4 1 |
45 |
|
(2)用茎叶图处理现有的数据不仅可以看出数据的分布状况,而且可以看出每组中的具
体数据.
(3)通过观察茎叶图,可以发现品种A的平均每亩产量为411.1千克,品种B的平均亩
产量为397.8千克.由此可知,品种A的平均亩产量比品种B的平均亩产量高.但品种A的
亩产量不够稳定,而品种B的亩产量比较集中D平均产量附近.
21.(2009全国卷Ⅱ文)(本小题满分12分)某车间甲组有10名工人,其中有4名女工人;
乙组有10名工人,其中有6名女工人。现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取4名工人进行技术考核。
(1)求从甲、乙两组各抽取的人数;
(2)求从甲组抽取的工人中恰有1名女工人的概率;
(3)求抽取的4名工人中恰有2名男工人的概率。
解析 本题考查概率统计知识,要求有正确理解分层抽样的方法及利用分类原理处理事件概率的能力,第一问直接利用分层统计原理即可得人数,第二问注意要用组合公式得出概率,第三问关键是理解清楚题意以及恰有2名男工人的具体含义,从而正确分类求概率.
解 (1)由于甲、乙两组各有10名工人,根据分层抽样原理,要从甲、乙两组中共抽
取4名工人进行技术考核,则从每组各抽取2名工人.
(2)记 表示事件:从甲组抽取的工人中恰有1名女工人,则
表示事件:从甲组抽取的工人中恰有1名女工人,则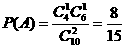
(3)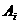 表示事件:从甲组抽取的2名工人中恰有
表示事件:从甲组抽取的2名工人中恰有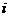 名男工人,
名男工人,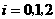
 表示事件:从乙组抽取的2名工人中恰有
表示事件:从乙组抽取的2名工人中恰有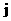 名男工人,
名男工人,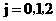
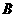 表示事件:抽取的4名工人中恰有2名男工人。
表示事件:抽取的4名工人中恰有2名男工人。
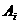 与
与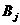 独立,
独立,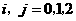 ,且
,且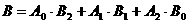
故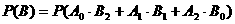
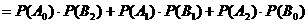
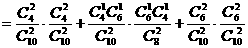
20.(2009山东卷文)(本小题满分12分)一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
|
|
轿车A |
轿车B |
轿车C |
|
舒适型 |
100 |
150 |
z |
|
标准型 |
300 |
450 |
600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值.
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
解 (1)设该厂本月生产轿车为n辆,由题意得,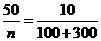 ,所以n=2000.
,所以n=2000.
z=2000-100-300-150-450-600=400
(2)设所抽样本中有m辆舒适型轿车,因为用分层抽样的方法在C类轿车中抽取一个容量
为5的样本,所以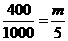 ,解得m=2也就是抽取了2辆舒适型轿车,3辆标准型轿车,分
,解得m=2也就是抽取了2辆舒适型轿车,3辆标准型轿车,分
别记作S1,S2;B1,B2,B3,则从中任取2辆的所有基本事件为(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1),
(S2 ,B2), (S2 ,B3),( (S1, S2),(B1 ,B2), (B2 ,B3) ,(B1 ,B3)共10个,其中至少有1辆舒适型轿车的基本
事件有7个基本事件: (S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),所以从中任取
2辆,至少有1辆舒适型轿车的概率为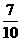 .
.
(3)样本的平均数为 ,
,
那么与样本平均数之差的绝对值不超过0.5的数为9.4, 8.6, 9.2, 8.7, 9.3, 9.0这6个数,总的个数为8,所以该数与样本平均数之差的绝对值不超过0.5的概率为 .
.
[命题立意]本题为概率与统计的知识内容,涉及到分层抽样以及古典概型求事件的概率
问题.要读懂题意,分清类型,列出基本事件,查清个数.,利用公式解答.
19.(2009广东卷理)(本小题满分12分)
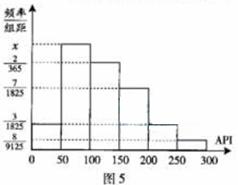 根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
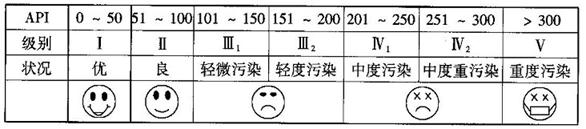 对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间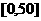 ,
,
 ,
,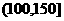 ,
,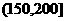 ,
,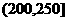 ,
,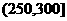 进行分组,得到频率分布
进行分组,得到频率分布
直方图如图5.
(1)求直方图中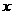 的值;
的值;
(2)计算一年中空气质量分别为良和轻微污染的天数;
(3)求该城市某一周至少有2天的空气质量为良或轻微污染的概率.
(结果用分数表示.已知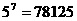 ,
,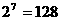 ,
,
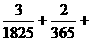

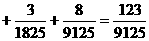 ,
, )
)
解 (1)由图可知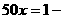
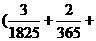

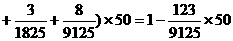 ,解得
,解得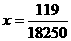 ;
;
(2)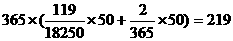 ;
;
(3)该城市一年中每天空气质量为良或轻微污染的概率为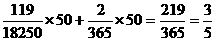 ,则空气质量不为良且不为轻微污染的概率为
,则空气质量不为良且不为轻微污染的概率为 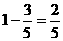 ,一周至少有两天空气质量为良或轻微污染的概率为
,一周至少有两天空气质量为良或轻微污染的概率为 .
.
18.(2009年广东卷文)(本小题满分13分)
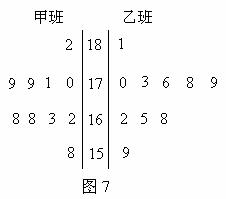 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图
如图7.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差
(3)现从乙班这10名同学中随机抽取两名身高不低于
173cm的同学,求身高为176cm的同学被抽中的概率.
解析
(1)由茎叶图可知:甲班身高集中于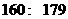
之间,而乙班身高集中于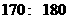 之间。因此乙班平
之间。因此乙班平
均身高高于甲班;
(2) 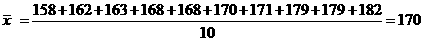
甲班的样本方差为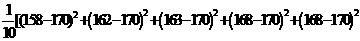
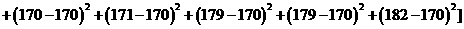 =57
=57
(3)设身高为176cm的同学被抽中的事件为A;
从乙班10名同学中抽中两名身高不低于173cm的同学有:(181,173) (181,176)
(181,178) (181,179) (179,173) (179,176) (179,178) (178,173)
(178, 176) (176,173)共10个基本事件,而事件A含有4个基本事件;
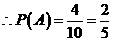 ;
;
17.(2009湖北卷理)样本容量为200的频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在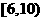 内的频数为 ,数据落在
内的频数为 ,数据落在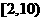 内的概率约为
.
内的概率约为
.
答案 64 0.4
解析 由于在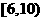 范围内频数、组距是0.08,所以频率是0.08*组距=0.32,而频数=
范围内频数、组距是0.08,所以频率是0.08*组距=0.32,而频数=
频率*样本容量,所以频数=(0.08*4)*200=64
同样在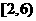 范围内的频数为16,所以在
范围内的频数为16,所以在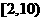 范围内的频数和为80,概率为80/200=0.4
范围内的频数和为80,概率为80/200=0.4
16.(2009重庆卷文)从一堆苹果中任取5只,称得它们的质量如下(单位:克)125 124
121 123 127则该样本标准差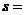 (克)(用数字作答).
(克)(用数字作答).
答案 2
解析 因为样本平均数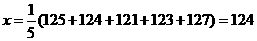 ,
,
则样本方差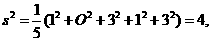 所以
所以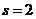
15.(2009天津卷理)某学院的A,B,C三个专业共有1200名学生,为了调查这些学生勤
工俭学的情况,拟采用分层抽样的方法抽取一个容量为120的样本。已知该学院的A专业有380名学生,B专业有420名学生,则在该学院的C专业应抽取____名学生。
答案 40
解析 C专业的学生有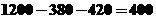 ,由分层抽样原理,
,由分层抽样原理,
应抽取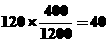 名.
名.
14.(2009湖南卷理)一个总体分为A,B两层,其个体数之比为4:1,用分层抽样方法从总体中抽取一个容量为10的样本,已知B层中甲、乙都被抽到的概率为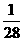 ,则总体中的个数数位 .
,则总体中的个数数位 .
答案 40
解析
由条件易知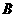 层中抽取的样本数是2,设
层中抽取的样本数是2,设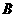 层总体数是
层总体数是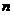 ,则又由
,则又由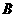 层中甲、乙都被抽到的概率是
层中甲、乙都被抽到的概率是 =
=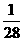 ,可得
,可得 ,所以总体中的个数是
,所以总体中的个数是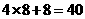 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com