
题目列表(包括答案和解析)
6.(2008广东理)某校共有学生2000名,各年级男、女生人数如下表.已知在全校 学生中随机抽取1名,抽到二年级女生的概率是0.19.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为 ( )
|
|
一年级 |
二年级 |
三年级 |
|
女生 |
373 |
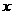 |
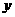 |
|
男生 |
377 |
370 |
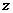 |
A.24 B.18 C.16 D.12
答案 C
解析 依题意我们知道二年级的女生有380人,那么三年级的学生的人数应该是 ,
,
即总体中各个年级的人数比例为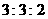 ,故在分层抽样中应在三年级抽取的学生人数为
,故在分层抽样中应在三年级抽取的学生人数为

5、(2008山东文)从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为( )
|
分数 |
5 |
4 |
3 |
2 |
1 |
|
人数 |
20 |
10 |
30 |
30 |
10 |
A.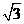 B.
B.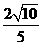 C.3 D.
C.3 D.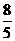
答案 B
解析 本小题主要考查平均数、方差、标准差的概念及其运算.


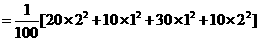
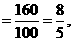

4.(2008湖南)对有n(n≥4)个元素的总体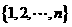 进行抽样,先将总体分成两个子总体
进行抽样,先将总体分成两个子总体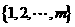 和
和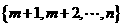 (m是给定的正整数,且2≤m≤n-2),再从每个子总体中各随机抽取2个元素组成样本.用
(m是给定的正整数,且2≤m≤n-2),再从每个子总体中各随机抽取2个元素组成样本.用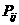 表示元素i和j同时出现在样本中的概率,则
表示元素i和j同时出现在样本中的概率,则 = ; 所有
= ; 所有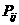 (1≤i<j≤
(1≤i<j≤ 的和等于 .
的和等于 .
答案 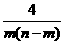 ,6
,6
3.(2008上海)已知总体的各个体的值由小到大依次为2,3,3,7,a,b,12,13.7,18.3,20,且总体的中位数为10.5,若要使该总体的方差最小,则a、b的取值分别是
答案 10.5和10.5
2.(2008天津)一个单位共有职工200人,其中不超过45岁的有120人,超过45岁的有
80人.为了调查职工的健康状况,用分层抽样的方法从全体职工中抽取一个容量为25的样本,应抽取超过45岁的职工________________人.
答案 10
1、(2008山东理)右图是根据《山东统计年整2007》中的资料作成
的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图
中左边的数字从左到右分别表示城镇居民百户家庭人口数的百
位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的
个位数字,从图中可以得到1997年至2006年我省城镇居民百户
家庭人口数的平均数为 ( )
A.304.6 B.303.6 C.302.6 D.301.6
答案 B
解析 本题考查茎叶图、用样本数字特征估计总体特征。
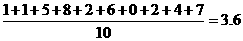
27.(2009宁夏海南卷文)(本小题满分12分)某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(1)A类工人中和B类工人各抽查多少工人?
(2)从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1:
|
生产能力分组 |
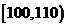 |
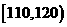 |
 |
 |
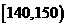 |
|
人数 |
4 |
8 |
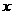 |
5 |
3 |
表2:
|
生产能力分组 |
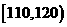 |
 |
 |
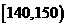 |
|
人数 |
6 |
y |
36 |
18 |
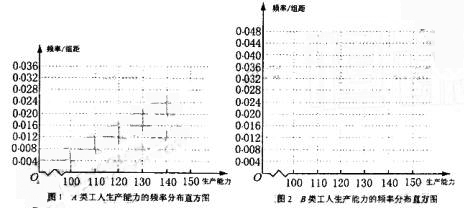
(1)先确定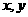 ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中
个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察
直方图直接回答结论)
(2)分别估计 类工人和
类工人和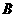 类工人生产能力的平均数,并估计该工厂工人和生产能力的平
类工人生产能力的平均数,并估计该工厂工人和生产能力的平
均数(同一组中的数据用该区间的中点值作代表)。
解 (1) 类工人中和
类工人中和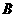 类工人中分别抽查25名和75名.
类工人中分别抽查25名和75名.
(2)(ⅰ)由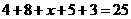 ,得
,得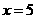 ,
,
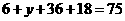 ,得
,得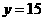 .
.
频率分布直方图如下
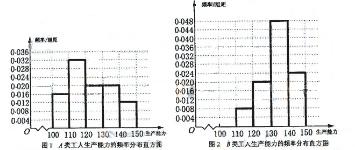
从直方图可以判断: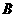 类工人中个体间的差异程度更小.
类工人中个体间的差异程度更小.
(2) 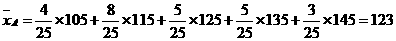 ,
,
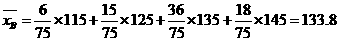 ,
,
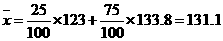
A类工人生产能力的平均数,B类工人生产能力的平均数以及全厂工人生产能力的平均
数的估计值分别为123,133.8和131.1.
2005-2008年高考题
26.(2009辽宁文)(本小题满分12分)某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸,的结果如下表:
甲厂
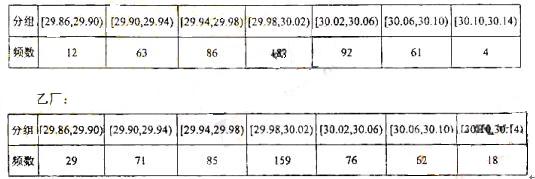 试分别估计两个分厂生产的零件的优质品率;
试分别估计两个分厂生产的零件的优质品率;
(1)由于以上统计数据填下面 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
|
|
甲 厂 |
乙 厂 |
合计 |
|
优质品 |
|
|
|
|
非优质品 |
|
|
|
|
合计 |
|
|
|
附:
解 (1)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为
 ;
;
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为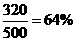
(2)
|
|
甲厂 |
乙厂 |
合计 |
|
优质品 |
360 |
320 |
680 |
|
非优质品 |
140 |
180 |
320 |
|
合计 |
500 |
500 |
1000 |

所以有99%的把握认为“两个分厂生产的零件的质量有差异”。
25.(2009宁夏海南卷理)(本小题满分12分)某工厂有工人1000名, 其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)。
(1)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人;
(2)从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2.
表1
|
生产能力分组 |
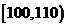 |
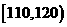 |
 |
 |
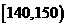 |
|
人数 |
4 |
8 |
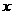 |
5 |
3 |
表2
|
生产能力分组 |
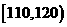 |
 |
 |
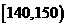 |
|
人数 |
6 |
y |
36 |
18 |
(1)先确定x,y,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
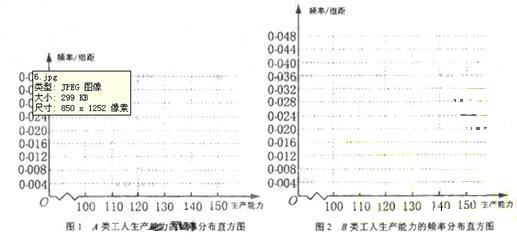
(2)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数,同一组中的数据用该组区间的中点值作代表)
解 (1)甲、乙被抽到的概率均为 ,且事件“甲工人被抽到”与事件“乙工人被抽到”相互独立,故甲、乙两工人都被抽到的概率为
,且事件“甲工人被抽到”与事件“乙工人被抽到”相互独立,故甲、乙两工人都被抽到的概率为
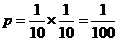 .
.
(2)(i)由题意知A类工人中应抽查25名,B类工人中应抽查75名.
故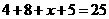 ,得
,得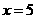 ,
,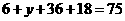 ,得
,得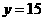 .
.
频率分布直方图如下
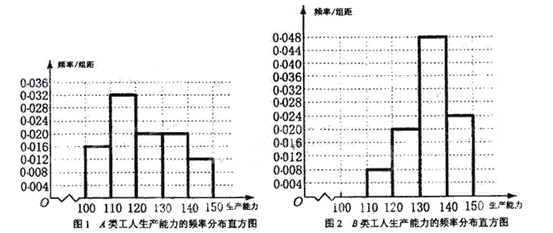 从直方图可以判断:B类工人中个体间的关异程度更小 .
从直方图可以判断:B类工人中个体间的关异程度更小 .
(ii)
 ,
,
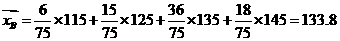 ,
,
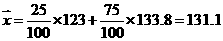
A类工人生产能力的平均数,B类工人生产能力的平均数以及全工厂工人生产能力的
平均数的会计值分别为123,133.8和131.1 .
24.(2009全国卷Ⅱ理)(本小题满分12分)某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核。
(1)求从甲、乙两组各抽取的人数;
(I2)求从甲组抽取的工人中恰有1名女工人的概率;
(3)记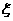 表示抽取的3名工人中男工人数,求
表示抽取的3名工人中男工人数,求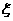 的分布列及数学期望。
的分布列及数学期望。
分析 (1)这一问较简单,关键是把握题意,理解分层抽样的原理即可。另外要注意
此分层抽样与性别无关。
(2)在第一问的基础上,这一问处理起来也并不困难。
从甲组抽取的工人中恰有1名女工人的概率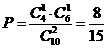
(3)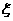 的可能取值为0,1,2,3
的可能取值为0,1,2,3
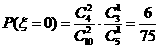 ,
, ,
,
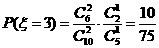 ,
,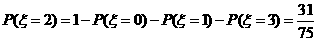
分布列及期望略.
评析:本题较常规,比08年的概率统计题要容易。在计算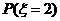 时,采用分类的方
时,采用分类的方
法,用直接法也可,但较繁琐,考生应增强灵活变通的能力。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com