
题目列表(包括答案和解析)
2010年联考题
31.(湖北卷)某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加了其中一组。在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%。登山组的职工占参加活动总人数的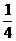 ,且该组中,青年人占50%,中年人占40%,老年人占10%。为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本。试确定
,且该组中,青年人占50%,中年人占40%,老年人占10%。为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本。试确定
(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数。
本小题主要考查分层抽样的概念和运算,以及运用统计知识解决实际问题的能力.
解 (1)设登山组人数为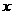 ,游泳组中,青年人、中年人、老年人各占比例分别为a、b、c,则有
,游泳组中,青年人、中年人、老年人各占比例分别为a、b、c,则有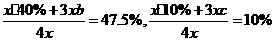 ,解得b=50%,c=10%.
,解得b=50%,c=10%.
故a=100%-50%-10%=40%,即游泳组中,青年人、中年人、老年人各占比例分别为40%、
50%、10%。
(2)游泳组中,抽取的青年人数为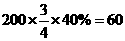 (人);抽取的中年人数为
(人);抽取的中年人数为
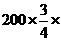 50%=75(人);抽取的老年人数为
50%=75(人);抽取的老年人数为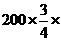 10%=15(人)。
10%=15(人)。
0.7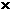 100+0.35=70.35
100+0.35=70.35
故耗能减少了90-70.35=19.65(吨)
30.(2007广东理)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量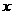 (吨)与相应的生产能耗
(吨)与相应的生产能耗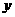 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
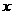
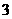
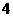
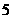
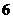
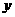
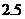
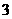
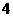
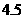
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出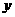 关于
关于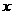 的线性回归方程
的线性回归方程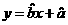 ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性
回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值: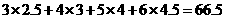 )
)
解 (1)如下图
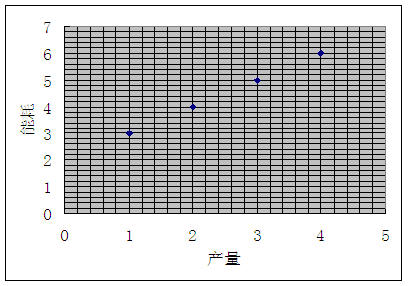
(2)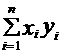 =3
=3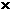 2.5+4
2.5+4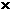 3+5
3+5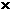 4+6
4+6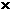 4.5=66.5
4.5=66.5
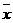 =
=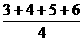 =4.5
=4.5
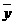 =
=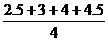 =3.5
=3.5
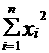 =
=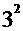 +
+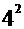 +
+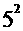 +
+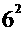 =86
=86

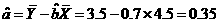
故线性回归方程为y=0.7x+0.35
(3)根据回归方程的预测,现在生产100吨产品消耗的标准煤的数量为
29.(2007湖南文)(本小题满分12分)在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如右表:
(1)在答题卡上完成频率分布表,并在给定的坐标系中画出频率分布直方图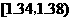 ;
;
(2)估计纤度落在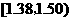 中的概率及纤度小于
中的概率及纤度小于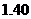 的概率是多少?
的概率是多少?
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间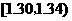 的中点值
的中点值
是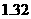 )作为代表.据此,估计纤度的期望.
)作为代表.据此,估计纤度的期望.
|
分组 |
频数 |
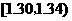 |
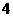 |
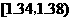 |
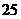 |
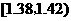 |
 |
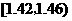 |
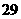 |
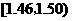 |
 |
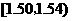 |
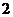 |
|
合计 |
 |
解 (Ⅰ)
|
分组 |
频数 |
频率 |
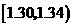 |
4 |
0.04 |
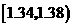 |
25 |
0.25 |
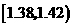 |
30 |
0.30 |
 |
29 |
0.29 |
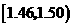 |
10 |
0.10 |
|
|
2 |
0.02 |
|
合计 |
100 |
1.00 |
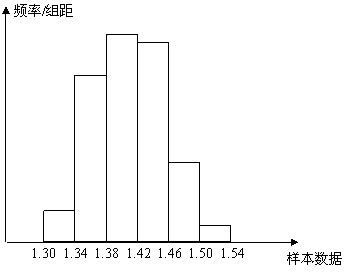
(Ⅱ)纤度落在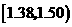 中的概率约为
中的概率约为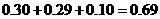 ,纤度小于1.40的概率约为
,纤度小于1.40的概率约为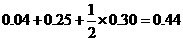 .
.
(Ⅲ)总体数据的期望约为
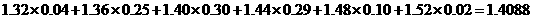
28.(2007湖南文)根据某水文观测点的历史统计数据,得到某条河流水位的频率分布直方图(如图2).从图中可以看出,该水文观测点平均至少一百年才遇到一次的洪水的最低水位是 ( )
A.48米 B.49米 C.50米 D.51米
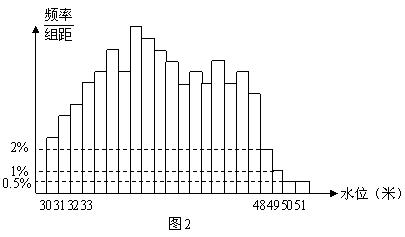

答案 C
27.(2007辽宁文)(本小题满分12分)某公司在过去几年内使用某种型号的灯管1000支,该公司对这些灯管的使用寿命(单位:小时)进行了统计,统计结果如下表所示:
|
分组 |
[500,900) |
[900,1100) |
[1100,1300) |
[1300,1500) |
[1500,1700) |
[1700,1900) |
[1900, ) ) |
|
频数 |
48 |
121 |
208 |
223 |
193 |
165 |
42 |
|
频率 |
|
|
|
|
|
|
|
(1)将各组的频率填入表中;
(2)根据上述统计结果,计算灯管使用寿命不足1500小时的频率;
(3)该公司某办公室新安装了这种型号的灯管3支,若将上述频率作为概率,试求至少
有2支灯管的使用寿命不足1500小时的概率.
解 (1)
|
分组 |
[500,900) |
[900,1100) |
[1100,1300) |
[1300,1500) |
[1500,1700) |
[1700,1900) |
[1900, ) ) |
|
频数 |
48 |
121 |
208 |
223 |
193 |
165 |
42 |
|
频率 |
0.048 |
0.121 |
0.208 |
0.223 |
0.193 |
0.165 |
0.042 |
(2)由(1)可得 ,所以灯管使用寿命不足1500小时的频率为0.6.
,所以灯管使用寿命不足1500小时的频率为0.6.
(3)由(II)知,1支灯管使用寿命不足1500小时的概率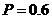 ,根据在
,根据在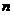 次独立重复试验中事件恰好发生
次独立重复试验中事件恰好发生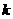 次的概率公式可得
次的概率公式可得
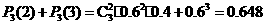 .
.
所以至少有2支灯管的使用寿命不足1500小时的概率是0.648. 12分
26.(2007宁夏)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗Y(吨标准煤)的几组对照数据
|
|
3 |
4 |
5 |
6 |
|
y |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,崩最小二乘法求出Y关于x的线性回归方程Y=bx+a;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性
同归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
解 (1)如图
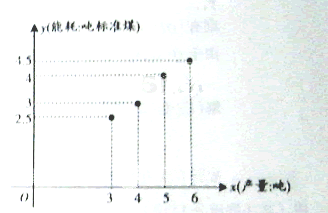
(2)由对照数据,计算得: 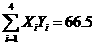

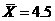 ,
, ;
;
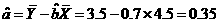
所求的回归方程为 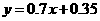
(3) 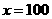 ,
, 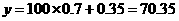 吨,
吨,
预测生产100吨甲产品的生产能耗比技改前降低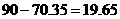 (吨)
(吨)
25.(2008辽宁)(本小题满分12分)某批发市场对某种商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:
|
周销售量 |
2 |
3 |
4 |
|
频数 |
20 |
50 |
30 |
(Ⅰ)根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
(Ⅱ)已知每吨该商品的销售利润为2千元,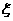 表示该种商品两周销售利润的和(单位:千元).若以上述频率作为概率,且各周的销售量相互独立,求
表示该种商品两周销售利润的和(单位:千元).若以上述频率作为概率,且各周的销售量相互独立,求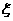 的分布列和数学期望.
的分布列和数学期望.
解 本小题主要考查频率、概率、数学期望等基础知识,考查运用概率知识解决实际
问题的能力.满分12分.
解 (Ⅰ)周销售量为2吨,3吨和4吨的频率分别为0.2,0.5和0.3.···· 3分
(Ⅱ)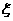 的可能值为8,10,12,14,16,且
的可能值为8,10,12,14,16,且
P(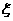 =8)=0.22=0.04,
=8)=0.22=0.04,
P(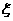 =10)=2×0.2×0.5=0.2,
=10)=2×0.2×0.5=0.2,
P(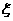 =12)=0.52+2×0.2×0.3=0.37,
=12)=0.52+2×0.2×0.3=0.37,
P(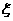 =14)=2×0.5×0.3=0.3,
=14)=2×0.5×0.3=0.3,
P(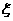 =16)=0.32=0.09.
=16)=0.32=0.09.
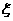 的分布列为
的分布列为
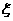 |
8 |
10 |
12 |
14 |
16 |
|
P |
0.04 |
0.2 |
0.37 |
0.3 |
0.09 |
··························· 9分
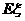 =8×0.04+10×0.2+12×0.37+14×0.3+16×0.09=12.4(千元)······ 12分
=8×0.04+10×0.2+12×0.37+14×0.3+16×0.09=12.4(千元)······ 12分
4.乙品种棉花的纤维长度基本上是对称的,而且大多集中在中间(均值附近).甲品种
棉花的纤维长度除一个特殊值(352)外,也大致对称,其分布较均匀.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com