
题目列表(包括答案和解析)
2.频率和概率
频率和概率都是学习的重点,也是学习的难点.频率是指在多次重复试验的基础上此事件发生的次数与试验总次数的比值,它随着试验次数的改变而变化,它不是常数,但它具有一定的稳定性,总在某个常数附近摆动,且随着试验次数的不断增大,这种摆动幅度越来越小.而上述中的常数是事件发生的概率,它不随着试验次数的改变而变化.(注:必然事件的频率与概率相等)
例2 判断下列命题的真假.
(1)掷100次硬币,出现正面的频率是0.4,则在试验中出现正面向上的次数为40次;
(2)某产品的次品率为3%,则任取该产品100件,其中必有3件次品.
(答案:(1)真;(2)假)
1.随机事件、必然事件与不可能事件
随机事件是指在一定条件下可能发生也可能不发生的事件;必然事件是指在一定条件下一定发生的事件,其概率为1;不可能事件是指在一定条件下一定不发生的事件,其概率为0.但需要注意,从概率学角度看,概率为1的事件可以是必然事件,也可以是随机事件;同样,概率为0的事件可以是不可能事件也可以是随机事件.
例1 从实数集中取出一个数,这个数是5的概率是( ).
(A)0 (B)1 (C)(0,1) (D)不确定
分析:记事件 为“取出的数是5”,很明显,“从实数集中取出一个数”这个试验有无数个可能的结果,所以
为“取出的数是5”,很明显,“从实数集中取出一个数”这个试验有无数个可能的结果,所以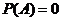 .而从试验本身来看,事件
.而从试验本身来看,事件 可能发生也可能不发生,所以事件
可能发生也可能不发生,所以事件 又是一个随机事件.综上所述,事件
又是一个随机事件.综上所述,事件 是一个概率为0的随机事件,所以选(A).
是一个概率为0的随机事件,所以选(A).
2.已知集合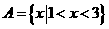 ,
,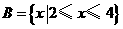 .若两集合之间的一种运算“
.若两集合之间的一种运算“ ”,使
”,使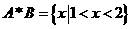 ,则
,则 .
.
答案:1.B 2. .
.
1.定义非空数集 的一种运算:
的一种运算: .若
.若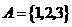 ,
,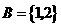 ,则
,则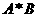 中的所有元素数字之和为( ).
中的所有元素数字之和为( ).
A.9 B.14 C.18 D.21
例3 同室四人各写一张贺卡,先集中起来,然后每人从中拿一张别人送出的贺卡,则四张贺卡的不同分配方式有多少种?
解法1:第一步:四个人中的任意一人先取一张,则由题意知共有3种取法;
第二步:由第一人取走的贺卡的供卡人取,也有3种取法;
第三步:由剩余的两人中的任一人取,只有一种取法;
第四步:最后一人取,只有一种取法.
由分步计数原理,共有3×3×1×1=9种方法.
解法2:设四张贺卡分别记为 ,由题意,某人(不妨设
,由题意,某人(不妨设 卡的供卡人)取卡的情况有3种,据此将卡的不同分配方式分为三类,对于每一类,其他人依次取卡分步进行,为了避免
卡的供卡人)取卡的情况有3种,据此将卡的不同分配方式分为三类,对于每一类,其他人依次取卡分步进行,为了避免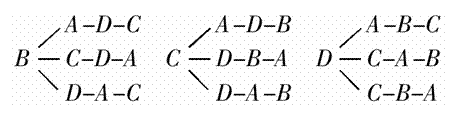 重复或遗漏现象,我们用“树形图”表示如下:
重复或遗漏现象,我们用“树形图”表示如下:
易知共有9种不同的分配方式.
评注:同一问题既可用分步计数原理,又可用分类计数原理,要针对具体情况灵活选择.
友情提示:1.在解决具体问题时,首先必须弄清楚是“分类”还是“分步”,接着要明确“分类”或者“分步”的具体标准是什么,简单地说“分类互斥”、“分步互依”,关键是看能否独立完成这件事.与此同时还要注意分类、分步不能重复,也不可遗漏.
2.对于较为复杂的既要用分类加法计数原理,又要用分步乘法计数原理的问题,我们可以根据题意恰当合理地画出示意图或者列出表格,使问题的实质直观地显示出来,从而便于我们解题.
例2 现要排一份5天的值班表,每天有一个人值班,共有5个人,每个人都可以值多天班或不值班,但相邻两天不准由同一个人值班,问此值班表共有多少种不同的排法?
分析:完成排值班表这件事,可逐天安排,分步进行,用分步计数原理求解.
解:先排第一天,可排5人中的任一人,有5种排法;再排第二天,此时不能排第一天已排的人,有4种排法;排第三天,此时不能排第二天已排的人,仍有4种排法;同理,第四、第五天均有4种排法,由分步计数原理可得值班表共有不同的排法数为:
5×4×4×4×4=1280种.
答:值班表共有1280种不同的排法.
 注意:此题与2003年新课程卷文科第16题不同:将3种作物种植在如图的5块试验田里,每块种植一种作物且相邻的试验田不能种植同一作物,不同的种植方法共有_____种(以数字作答).
注意:此题与2003年新课程卷文科第16题不同:将3种作物种植在如图的5块试验田里,每块种植一种作物且相邻的试验田不能种植同一作物,不同的种植方法共有_____种(以数字作答).
若将答案写成3×2×2×2×2=48种,就忽略了3种作物都必须种植的隐含条件,多计算了 种方法.
种方法.
因此原问题应有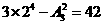 种不同的种植方法.
种不同的种植方法.
例1 在所有的两位数中,个位数字大于十位数字的两位数有多少个?
解:根据题意,将十位数上的数字分成8类,分别是1,2,3,4,5,6,7,8,在每一类中满足条件的两位数分别有8个,7个,6个,5个,4个,3个,2个,1个.由分类计数原理可知:符合题意的两位数的个数共有8+7+6+5+4+3+2+1=36个.
答:这样的两位数共有36个.
思考:同学们,你能换一种方法给出解答吗?(提示:从等可能出发, 个两位数有一半满足题意.)
个两位数有一半满足题意.)
例3 袋中放有3个伍分硬币,3个贰分硬币,4个壹分硬币,从中任意取出3个,求总币值超过8分的概率.
解:从10个硬币中取3个,共有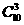 种方法,“总数超过8分”共有:
种方法,“总数超过8分”共有:
①取3个伍分硬币有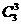 种;
种;
②取2个伍分,1个贰分,有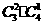 ;
;
③取到2个伍分硬币和1个壹分硬币,有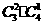 种;
种;
④取到1个伍分硬币和2个贰分硬币,有 种.
种.
故共有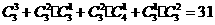 种,
种,
故总币值超过8分的概率为 .
.
注:由于本题分类情况较多,所以分类时一定要注意做到不重不漏.此题还可利用对立事件,同学们不妨一试.
例2 现有5个人,每个人都等可能的被分到8个房间中任意一间去住,求下列事件的概率:(1)指定的5个房间各有1人住;(2)恰好5个房间,其中各住1人;(3)某指定的房间中恰有3个人住.
分析:问题(1)是元素全排列问题;问题(2)须先选再排;问题(3)选出3人后再安排好余下的2人即可.
解:每个人都有8种分法且等可能,5个人被分到8个房间去住的分法,共有 种可能的分法.
种可能的分法.
(1)记 为“指定的5个房间各住1人”,
为“指定的5个房间各住1人”, 中包含
中包含 种分法,因此指定的5个房间各住1人的概率
种分法,因此指定的5个房间各住1人的概率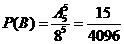 ;
;
(2)记“恰好有5个房间其中各住1人”为事件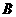 ,则
,则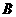 中包含
中包含 种分法,因此
种分法,因此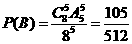 ;
;
(3)记“某指定房间恰有3人”为事件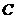 ,指定的房间住3人,有
,指定的房间住3人,有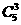 种分法,剩余2人中的每人可在7个房间中任选1间有
种分法,剩余2人中的每人可在7个房间中任选1间有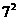 种选法,所以
种选法,所以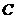 中包含
中包含 种不同的选法,因此
种不同的选法,因此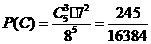 .
.
注:本题模型为分球入盒问题.此模型有两类:①球有区别;②球无区别.盒子(位置)各不同,元素(球)相同与不同的解法自不相同.
例1 (1)在某次花样滑冰比赛中,发生裁判受贿事件,竞赛委员会决定将裁判由原来的9名增至14名,但只任取7名裁判的评分为有效分,若14名裁判中2人受贿,则有效分中没有受贿裁判的评分的概率是__________.
(2)从甲、乙、丙三人中任选两名为代表,甲被选中的概率为______.
(3)若以连续掷两次骰子分别得到的点数 作为点
作为点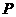 的坐标,则点
的坐标,则点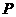 落在圆
落在圆 内的概率是________________.
内的概率是________________.
解析:(1)(直接法)依题意,所求的概率为 .
.
(间接法) .
.
(2)所有等可能结果为(甲,乙)、(甲,丙)、(乙,丙),共有3个,甲被选中的事件有2个,由等可能事件的概率计算得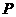 (甲)
(甲) .
.
(3)连续两次掷骰子一共有6×6=36个点,由于点落在圆 内,从而符合条件的点
内,从而符合条件的点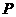 坐标为:(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(2,3)、(3,1)、(3,2)共8个,故所求的概率为
坐标为:(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(2,3)、(3,1)、(3,2)共8个,故所求的概率为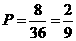 .
.
注:本题三个问题都属于摸球问题,广泛存在于生产和生活中,是等可能事件,可直接应用概率公式进行“计算”.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com