
题目列表(包括答案和解析)
1.用平均数估计总体
详释:(这是重点)平均数受样本中的每一个数据的影响,代表了总体的平均水平.
例1 在一批试验田里对某种早稻品种进行丰产栽培试验,抽测了其中14块试验田的单位面积(单位面积的大小为 )的产量如下(产量的单位为kg):
)的产量如下(产量的单位为kg):
504 402 495 500 501 405 409
460 486 460 371 420 456 395
这批试验田的平均单位面积产量约是多少?
解:如果将这批试验田里每块试验田的单位面积产量的全体称为总体,那么所抽测的14块试验田的单位面积产量就组成从这个总体中抽取的一个样本.于是我们可以用这个样本的平均数对相应的总体平均数作出估计.
用科学计算器算得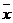 ≈447,
≈447,
即这14块试验田的平均产量为447kg,于是可以由此估计,这批试验田的平均单位面积产量约为447kg.
规律总结:常用两个样本平均数的大小去近似地比较相应两个总体平均数的大小.
例5 (2005年高考湖南卷试题)已知数列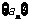 满足
满足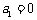 ,
,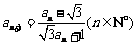 ,则
,则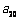 等于( )
等于( )
A.0 B.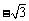 C.
C.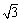 D.
D.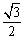
解析:令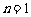 ,则
,则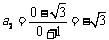 ;
;
令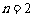 ,则
,则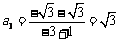 ;
;
令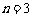 ,则
,则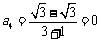 .
.
由此发现 ,可猜想此数列具有周期性,
,可猜想此数列具有周期性,
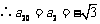 .故选B.
.故选B.
点评:由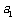 及递推关系先求出前几项,再归纳、猜想出
及递推关系先求出前几项,再归纳、猜想出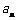 ,这一方法比较适用于选择、填空题.对于解答题,猜想出
,这一方法比较适用于选择、填空题.对于解答题,猜想出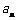 后,还应进一步证明(比如用数学归纳法).
后,还应进一步证明(比如用数学归纳法).
对某些递推数列问题,如果能透过其局部从整体着手,利用整体代入,往往能收到事半功倍之效.
例4
在数列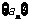 中,
中,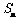 为其前
为其前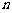 项和,若
项和,若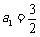 ,
,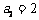 ,
,
并且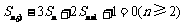 ,试判断
,试判断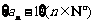 是不是等比数列?
是不是等比数列?
解析:将已知等式重新组合,得 ,即
,即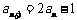 ,
,
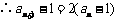 ,
,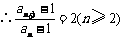 . (
. ( )
)
当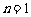 时,
时,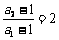 ,因此(
,因此( )式对
)式对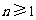 ,且
,且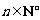 成立,
成立,
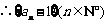 是等比数列.
是等比数列.
点评:从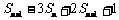 的整体着眼,将
的整体着眼,将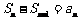 和
和 整体代入,解题过程则十分简洁、明快.
整体代入,解题过程则十分简洁、明快.
例3 某城市2009年末汽车保有量为30万辆,预计此后每年报废上一年末汽车保有量的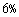 ,并且每年新增汽车数均为
,并且每年新增汽车数均为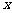 万辆.求
万辆.求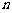 年后汽车的保有量.
年后汽车的保有量.
解析:从2001年起,该市每年末汽车保有量依次记为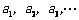 (单位:万辆),则可以得到数列
(单位:万辆),则可以得到数列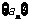 .
.
依题意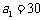 ,当
,当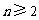 时,
时,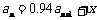 . ①
. ①
设 ,即
,即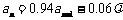 . ②
. ②
①,②比较,得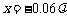 ,故
,故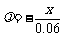 .
.
则数列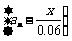 是首项为
是首项为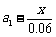 ,公比为0.94的等比数列.
,公比为0.94的等比数列.
所以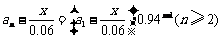 ,
,
即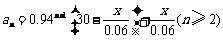 .
.
点评:形如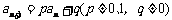 的递推数列求通项,适用此法.一般步骤是:令
的递推数列求通项,适用此法.一般步骤是:令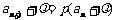 ,即
,即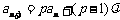 ,与已知递推数列比较得出
,与已知递推数列比较得出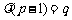 ,于是
,于是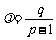 .从而转化为
.从而转化为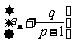 是公比为
是公比为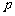 的等比数列再求解.
的等比数列再求解.
例2 设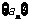 是首项为1的正项数列,且满足
是首项为1的正项数列,且满足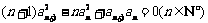 ,则它的通项公式
,则它的通项公式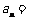 .
.
解析:由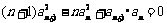 ,得
,得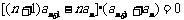 .
.
由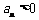 ,得
,得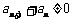 ,
,
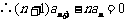 ,即
,即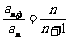 .
.
所以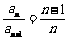 ,
,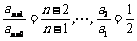 .
.
将以上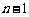 个式子累乘,得
个式子累乘,得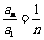 .
.
因为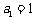 ,所以
,所以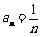 .
.
点评:形如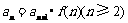 的递推数列求通项适用此法.
的递推数列求通项适用此法.
例1(高考广东卷试题)设平面内有n条直线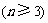 ,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用
,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用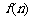 表示这
表示这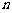 条直线交点的个数,则
条直线交点的个数,则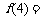 ;
;
当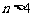 时,
时,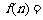 (用
(用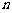 表示).
表示).
解析: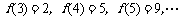 ,每增加一条直线,交点增加的个数等于原来直线的条数,所以
,每增加一条直线,交点增加的个数等于原来直线的条数,所以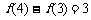 ,
,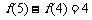 ,
, ,
,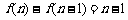 .
.
累加,得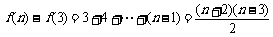 ,
,
所以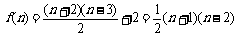 .
.
点评:形如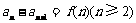 的递推数列适用此法求通项.
的递推数列适用此法求通项.
主要有知图定式、知式定图、图象变换等问题,运用单调性、过特殊点及图象变换规律来解决.
例5 (全国高考福建卷)把下面不完整的命题补充完整,并使之成为真命题:
若函数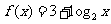 的图象与
的图象与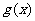 的图象关于 对称,则函数
的图象关于 对称,则函数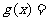 .(注:填上你认为可以成为真命题的一种情形即可,不必考虑所有可能的情形为真命题的一种情形即可,不必考虑所有可能的情形)
.(注:填上你认为可以成为真命题的一种情形即可,不必考虑所有可能的情形为真命题的一种情形即可,不必考虑所有可能的情形)
解:运用常用对称结论:
若关于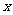 轴对称,则用
轴对称,则用 分别代替原函数中的
分别代替原函数中的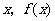 ,可得
,可得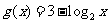 ;
;
若关于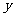 轴对称,则用
轴对称,则用 分别代替原函数中的
分别代替原函数中的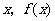 ,可得
,可得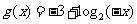 ;
;
若关于原点对称,则用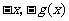 分别代替原函数中的
分别代替原函数中的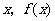 ,可得
,可得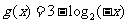 ;
;
若关于 对称,则用
对称,则用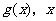 分别代替原函数中的
分别代替原函数中的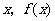 ,可得
,可得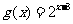 等等.
等等.
主要是有关指、对数函数的逆向求解,如已知单调性求参数范围,已知函数值求自变量,已知恒成立求参数等.
例4 (全国高考卷Ⅰ)设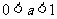 ,函数
,函数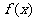
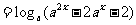 ,则使
,则使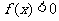 的
的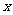 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C.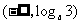 D.
D.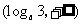
解:由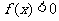 ,得
,得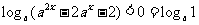 ,又
,又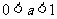 ,故
,故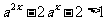 ,
,
解得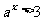 或
或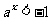 (舍去),所以
(舍去),所以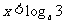 .
.
故选(C).
主要是判断增减性,求单调区间,利用单调性比较大小等.
例3 (全国高考卷Ⅲ)若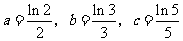 ,则( )
,则( )
A.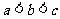 B.
B.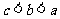 C.
C.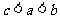 D.
D.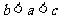
解法1:(转化法)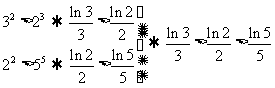 .
.
故选(C).
解法2:(作差法)
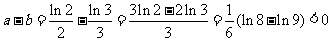 ,
,
所以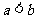 ;同理可得
;同理可得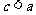 ,所以
,所以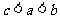 .
.
故选(C).
在处理反函数问题时,常常运用指、对数式的互化来解决,主要有以下两类:
(1)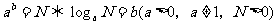 ,经常还伴随着对数运算性质的应用;
,经常还伴随着对数运算性质的应用;
(2)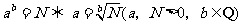 ,经常还伴随着幂运算性质的应用.
,经常还伴随着幂运算性质的应用.
例2 (2005全年全国高考江苏卷)函数 的反函数的解析表达式为( )
的反函数的解析表达式为( )
A.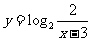 B.
B.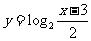
C.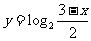 D.
D.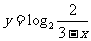
解:由已知得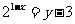 ,运用指、对数式的互化,得
,运用指、对数式的互化,得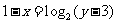 ,
,
所以其反函数的解析式为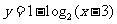 ,即
,即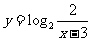 .
.
故选(A).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com