
题目列表(包括答案和解析)
9.半径为2的半圆纸片卷成圆锥放在桌面上,一阵风吹倒它,它的最高处距桌面 ( )
A.4 cm B.2 cm C.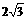 cm D.
cm D.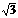 cm
cm
 11.函数f(x)满足
11.函数f(x)满足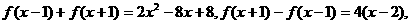 且
且
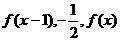 成等差数列,则x的值是( )
成等差数列,则x的值是( )
A.2 B.3
C.2和3 D.2和-3
8.圆锥的侧面展开图是圆心角为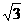 π的扇形,侧面积为2
π的扇形,侧面积为2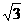 π,则过两条母线的截面的
π,则过两条母线的截面的
最大面积为 ( )
A.2 B.3 C. D.
D.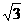
6.已知正三棱锥两个相邻侧面所成二面角为θ,那么θ的取值范围 ( )
A.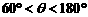 B.
B.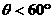 C.
C.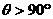 D.
D.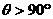 或
或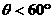
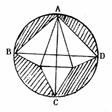 7.将半径为R的圆剪去如图所示的阴影部分(AC,BD为圆的直径),沿图所画的线折成一个正三棱锥,这个正三棱锥铡面与底面所成的二面角的余弦值是 ( )
7.将半径为R的圆剪去如图所示的阴影部分(AC,BD为圆的直径),沿图所画的线折成一个正三棱锥,这个正三棱锥铡面与底面所成的二面角的余弦值是 ( )
A.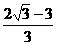 B.
B.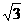 -2
-2
C.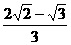 D.
D.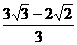
5.已知过球面上三点A、B、C的截面和球心的距离等于球半径R的一半,且AB=BC=CA=2, 则球面积S=4πR2= ( )
A.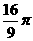 B.
B.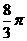 C.4π D.
C.4π D.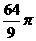
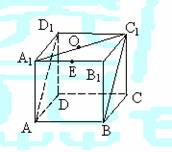
4.(05年高考湖南卷)如图,正方体ABCD-A1B1C1D1的棱长 为1,E是A1B1的中点,则E到平面AB C1D1的距离为( )
A.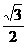 B.
B.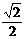
C.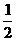 D.
D.
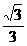
3.正方体ABCD-A1B1C1D1,E,F分别是正方形A1B1C1D1和
ADD1A1的中心,则EF和CD所成的角是 ( )
A.60° B.45°
 C.30° D.90°
C.30° D.90°
2.在空间四边形ABCD各边上分别取E、F、G、H四点,如果EF与GH能相交于点P,那么 ( )
A.点P必在直线AC上
 B.点P必在直线BD上
B.点P必在直线BD上
C.点P必在平面ABC内
D.点P必在平面ABC外
1.空间四点A、B、C、D,若直线AB⊥CD,AC⊥BD,AD⊥BC同时成立,则A、B、C、D四点的位置关系是 ( )
A.一定共面 B.不一定共面 C.一定不共面 D.这样的四点不存在
12.根据定义证明函数的单调性时,规范格式是什么?(取值, 作差, 判正负 );根据导数法研究函数单调性时,一定要注意“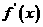 >0(或
>0(或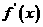 <0)是该函数在给定区间上单调递增(减)的必要条件
<0)是该函数在给定区间上单调递增(减)的必要条件
13 你知道函数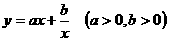 的单调区间吗?(该函数在
的单调区间吗?(该函数在 或
或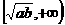 上单调递增;在
上单调递增;在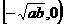 或
或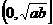 上单调递减)这可是一个应用广泛的函数!
上单调递减)这可是一个应用广泛的函数!
14 切记f(0)=0是定义在R上的y=f(x)为奇函数的必要条件
15 抽象函数的单调性、奇偶性一定要紧扣函数性质利用单调性、奇偶性的定义求解 同时,要领会借助函数单调性利用不等关系证明等式的重要方法:f(a)≥b 且f(a)≤bÛf(a)=b
16 对数函数问题时,你注意到真数与底数的限制条件了吗?(真数大于零,底数大于零且不等于1)字母底数还需讨论呀
17 数的换底公式及它的变形,你掌握了吗?(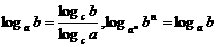 )
)
18 你还记得对数恒等式吗?(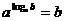 )
)
19 “实系数一元二次方程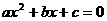 有实数解”转化为“
有实数解”转化为“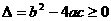 ”,你是否注意到必须
”,你是否注意到必须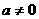 ;当a=0时,“方程有解”不能转化为
;当a=0时,“方程有解”不能转化为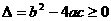 .若原题中没有指出是“二次”方程、函数或不等式,你是否考虑到二次项系数可能为零的情形?
.若原题中没有指出是“二次”方程、函数或不等式,你是否考虑到二次项系数可能为零的情形?
20 等差数列中的重要性质: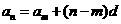 ;若
;若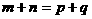 ,则
,则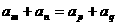
21 等比数列中的重要性质: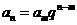 ;若
;若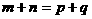 ,则
,则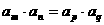 .
.
22 你是否注意到在应用等比数列求前n项和时,需要分类讨论.(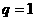 时,
时,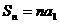 ;
;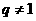 时,
时,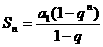 )
)
23 无穷递缩等比数列所有项和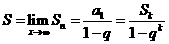 (0<|q|<1)
(0<|q|<1)
24 等比数列的一个求和公式:设等比数列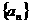 的前n项和为
的前n项和为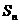 ,公比为
,公比为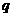 , 则
, 则
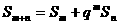 .
.
25 等差数列的一个性质:设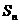 是数列
是数列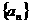 的前n项和,
的前n项和,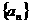 为等差数列的充要条件是
为等差数列的充要条件是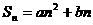 (a, b为常数)其公差是2a
(a, b为常数)其公差是2a
26 你知道怎样的数列求和时要用“错位相减”法吗?(若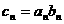 ,其中
,其中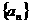 是等差数列,
是等差数列,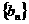 是等比数列,求
是等比数列,求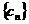 的前n项的和)
的前n项的和)
27 用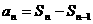 求数列的通项公式时,
求数列的通项公式时,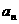 一般是分段形式对吗?你注意到
一般是分段形式对吗?你注意到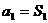 了吗?
了吗?
28 你还记得裂项求和吗?(如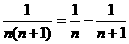 );
);
29 叠加法: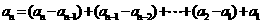 ;
;
30 叠乘法: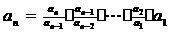
31 你知道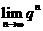 的结果吗?需要讨论吗?
的结果吗?需要讨论吗? 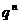 有极限时,则
有极限时,则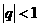 或
或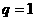 ,在求数列
,在求数列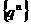 的极限时,你注意到q=1时,
的极限时,你注意到q=1时, 这种特例了吗?(例如:数列的通项公式为
这种特例了吗?(例如:数列的通项公式为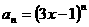 ,若
,若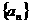 的极限存在,求x的取植范围 正确答案为
的极限存在,求x的取植范围 正确答案为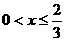 )
)
32 若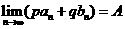 ,
,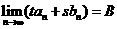 ,则求
,则求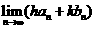 时能否用由
时能否用由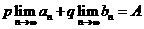 ,
,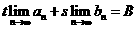 解方程组得
解方程组得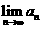 、
、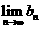 而获解?
而获解?
33 数列单调性问题能否等同于对应函数的单调性问题?(数列是特殊函数,但其“定义域”中的值不是连续的 )
34 在解三角问题时,你注意到正切函数、余切函数的定义域了吗?你注意到正弦函数、余弦函数的有界性了吗?在△ABC中,sinA>sinBÛA>B对吗?
35 一般说来,周期函数加绝对值或平方,其周期减半.(如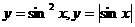 的周期都是
的周期都是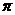 , 但
, 但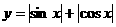 及
及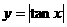 的周期为
的周期为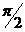 ,)
,)
36 函数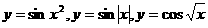 是周期函数吗?(都不是)
是周期函数吗?(都不是)
37 正弦曲线、余弦曲线、正切曲线的对称轴、对称中心你知道吗?
38 在三角中,你知道1等于什么吗?
(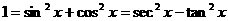
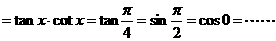
这些统称为1的代换) 常数 “1”的种种代换有着广泛的应用.
39 在三角的恒等变形中,要特别注意角的各种变换.(如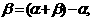
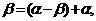
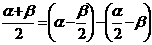 等)
等)
40 你还记得三角化简题的要求是什么吗?项数最少、函数种类最少、分母不含三角函数、且能求出值的式子,一定要算出值来)
41 你还记得三角化简的通性通法吗?(从函数名、角、运算三方面进行差异分析,常用的技巧有:切割化弦、降幂公式、用三角公式转化出现特殊角 异角化同角,异名化同名,高次化低次)
42 你还记得某些特殊角的三角函数值吗?
( )
)
43 你还记得在弧度制下弧长公式和扇形面积公式吗?(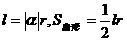 )
)
44 辅助角公式: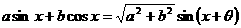 (其中
(其中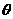 角所在的象限由a, b 的符号确定,
角所在的象限由a, b 的符号确定,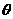 角的值由
角的值由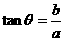 确定)在求最值、化简时起着重要作用
确定)在求最值、化简时起着重要作用
45 在用反三角函数表示直线的倾斜角、两向量的夹角、两条异面直线所成的角等时,你是否注意到它们各自的取值范围及意义?
①异面直线所成的角、直线与平面所成的角、二面角的取值范围依次是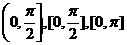
②直线的倾斜角、 到
到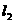 的角、
的角、 与
与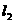 的夹角的取值范围依次是
的夹角的取值范围依次是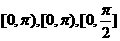 .
.
③向量的夹角的取值范围是[0,π]
46 若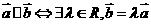 对吗?(
对吗?(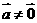 );
);
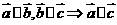 ,
, =
=
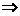
 ,
,  =0
=0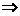
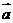 =0或
=0或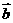 =0,
=0,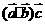 =
=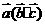 呢?
呢?
47 若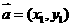 ,
,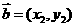 ,则
,则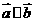 ,
,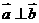 的充要条件是什么?
的充要条件是什么?
48 共线向量模相等是否等价于向量相等?
49 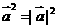 在已知向量长度求两向量夹角时注意用此关系整体求得数量积
在已知向量长度求两向量夹角时注意用此关系整体求得数量积
50 若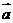 与
与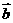 的夹角θ,且θ为钝角,则cosθ<0对吗?
的夹角θ,且θ为钝角,则cosθ<0对吗?
51 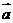 在
在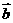 方向上的投影为
方向上的投影为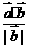 ;若
;若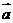 是与
是与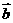 平行的向量,则
平行的向量,则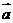 =
=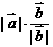
52 把y=f(x)图象向左移动|h|个单位,向上移动|k|个单位,则平移向量是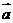 =(-|h|,|k|)
=(-|h|,|k|)
53 不等式的解集的规范书写格式是什么?(一般要写成集合的表达式)
54 分式不等式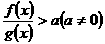 的一般解题思路是什么?(移项通分,零点分段)
的一般解题思路是什么?(移项通分,零点分段)
55 解无理不等式有哪几种常规题型?它们的等价不等式组是怎样的?
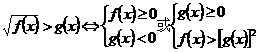 ;
; 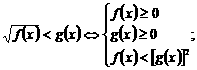
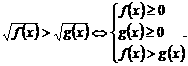
56 解指对不等式应该注意什么问题?(指数函数与对数函数的单调性, 对数的真数大于零 )
57 含有两个绝对值的不等式如何去绝对值?(一般是零点分段分类讨论)
58 利用重要不等式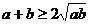 以及变式
以及变式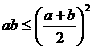 等求函数的最值时,你是否注意到a,b
等求函数的最值时,你是否注意到a,b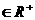 (或a ,b非负),且“等号成立”时的条件,积ab或和a+b其中之一应是定值?
(或a ,b非负),且“等号成立”时的条件,积ab或和a+b其中之一应是定值?
59 在解含有参数的不等式时,怎样进行讨论?(特别是指数和对数的底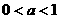 或
或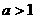 )讨论完之后,要写出:综上所述,原不等式的解是…….
)讨论完之后,要写出:综上所述,原不等式的解是…….
60 解含参数的不等式的通法是“定义域为前提,函数增减性为基础,分类讨论是关键.”
61 恒成立不等式问题通常解决的方法:借助相应函数的单调性求解,其主要技巧有数形结合法,分离变量法,主元法
62 直线方程的几种形式:点斜式、斜截式、两点式、截矩式、一般式.以及各种形式的局限性 (如点斜式不适用于斜率不存在的直线)
63 设直线方程时,一般可设直线的斜率为k,你是否注意到直线垂直于x轴时,斜率k不存在的情况?(例如:一条直线经过点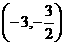 ,且被圆
,且被圆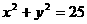 截得的弦长为8,求此弦所在直线的方程 该题就要注意,不要漏掉x+3=0这一解 )
截得的弦长为8,求此弦所在直线的方程 该题就要注意,不要漏掉x+3=0这一解 )
64 简单线性规划问题的可行域求作时,要注意不等式表示的区域是相应直线的上方、下方,是否包括边界上的点
65 对不重合的两条直线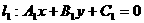 ,
,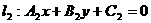 ,有
,有
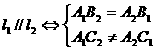 ;
;
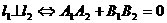 .
.
66 直线在坐标轴上的截距可正,可负,也可为0
67 直线在两坐标轴上的截距相等,直线方程可以理解为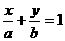 ,但不要忘记当 a=0时,直线y=kx在两条坐标轴上的截距都是0,也是截距相等.
,但不要忘记当 a=0时,直线y=kx在两条坐标轴上的截距都是0,也是截距相等.
68 处理直线与圆的位置关系有两种方法:(1)点到直线的距离;(2)直线方程与圆的方程联立,判别式 一般来说,前者更简捷.
69 处理圆与圆的位置关系,可用两圆的圆心距与半径之间的关系
70 在圆中,注意利用半径、半弦长、及弦心距组成的直角三角形
71 定比分点的坐标公式是什么?(起点,中点,分点以及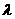 值可要搞清)
值可要搞清)
72 在利用定比分点解题时,你注意到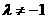 了吗?
了吗?
73 曲线系方程你知道吗?直线系方程?圆系方程?共焦点的椭圆系,共渐近线的双曲线系?
74 两圆相交所得公共弦方程是两圆方程相减消去二次项所得 x0x+y0y=r2 表示过圆x2+y2=r2上一点(x0,y0)的切线,若点(x0,y0)在已知圆外,x0x+y0y=r2 表示什么?(切点弦)
75 椭圆方程中三参数a、b、c的满足a2+b2=c2对吗?双曲线方程中三参数应满足什么关系?
76 椭圆中,注意焦点、中心、短轴端点所组成的直角三角形.(a,b,c)
77 若|PF1|+|PF2|=2a,则动点P的轨迹是以F1、F2为焦点的椭圆?若||PF1|-|PF2||=2a,则动点P的轨迹是以F1、F2为焦点的双曲线,对吗?
78 在解析几何中,研究两条直线的位置关系时,有可能这两条直线重合,而在立体几何中一般提到的两条直线可以理解为它们不重合
79 在利用圆锥曲线统一定义解题时,你是否注意到定义中的定比的分子分母的顺序?
80 在用圆锥曲线与直线联立求解时,消元后得到的方程中要注意:二次项的系数是否为零?判别式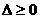 的限制.(求交点,弦长,中点,斜率,对称,存在性问题都在
的限制.(求交点,弦长,中点,斜率,对称,存在性问题都在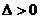 下进行)
下进行)
81 通径是抛物线的所有焦点弦中最短的弦
82 过抛物线y2=2px(p>0)焦点的弦交抛物线于A(x1,y1), B(x2,y2),则y1y2=-p2, x1x2=?,|AB|= x1+x2+p
83 若A(x1,y1), B(x2,y2)是二次曲线C:F(x,y)=0的弦的两个端点,则F(x1,y1)=0 且F(x2,y2)=0 涉及弦的中点和斜率时,常用点差法作F(x1,y1)-F(x2,y2)=0求得弦AB的中点坐标与弦AB的斜率的关系
84 作出二面角的平面角主要方法是什么?(定义法、三垂线法、垂面法)三垂线法:一定平面,二作垂线,三作斜线,射影可见
85 求点到面的距离的常规方法是什么?(直接法、体积变换法、向量法)
86 你知道三垂线定理的关键是什么吗?(一面、四线、三垂直、立柱即面的垂线是关键)一面四直线,立柱是关键,垂直三处见
87 立体几何中常用一些结论:正四面体的体积公式V=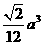 记住了吗?面积射影定理、“立平斜关系式”、最小角定理等你熟悉吗?
记住了吗?面积射影定理、“立平斜关系式”、最小角定理等你熟悉吗?
88 异面直线所成角利用“平移法”求解时,一定要注意平移后所得角是所求角或其补角
89 平面图形的翻折、立体图形的展开等一类问题,要注意翻折、展开前后有关几何元素的“不变量”与“不变性”
90 三棱錐的顶点在底面的射影何时为底面的内心、外心、垂心、重心?
91 解排列组合问题的依据是:分类相加,分步相乘,有序排列,无序组合.
92 解排列组合问题的规律是:元素分析法、位置分析法--相邻问题捆绑法;不邻问题插空法;多排问题单排法;定位问题优先法;多元问题分类法;有序分配问题法;选取问题先排后排法;至多至少问题间接法(或分类法).
93 二项式定理中,“系数最大的项”、“项的系数的最大值”、“项的二项式系数的最大值”是同一个概念吗?
94 求二项展开式各项系数代数和的有关问题中的“赋值法”、“转化法”,求特定项的“通项公式法”、“结构分析法”你会用吗?
95 “两个事件对立是这两个事件互斥的充分不必要条件 ”、“如果两个事件是相互独立事件,那么它们一定不是互斥事件 ”、“若A是一随机事件,则P(A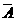 )= P(A)P(
)= P(A)P(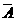 ) ”、“概率等于1的事件一定是必然事件,概率为零的事件一定是不可能事件 ”以上命题哪些是正确的呢?
) ”、“概率等于1的事件一定是必然事件,概率为零的事件一定是不可能事件 ”以上命题哪些是正确的呢?
96 公式P(A+B)= P(A)+P(B),P(AB)= P(A)P(B)的适用条件是什么?
97 用样本估计总体时,若两总体的期望相等,能否说两总体的“集中程度”一样?
98 假设检验中,依据的是实际推断原理:“小概率事件在一次试验中几乎不可能发生”推断的方法类似于通常使用的反证法
99 在数学归纳法归纳递推过程中,一定要注意从n=k到n=k+1时,相关的f(k)到f(k+1)时项的变化
100 函数y=f(x)在x=x0处连续,对y=f(x)有什么要求?
101 函数y=f(x)在x=x0处连续是函数y=f(x)在x=x0处可导的什么条件?
102 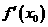 =0是可导函数y=f(x)在x=x0处有极值的必要条件,对吗?
=0是可导函数y=f(x)在x=x0处有极值的必要条件,对吗?
103 在复平面上,原点是不是虚轴上的点?虚轴上点的坐标特征是:(0,bi),是吗?
104 解直答题(选择题和填空题)的特殊方法是什么?(直接法,数形结合法,特殊化法,推理分析法,排除法,验证法,估算法等等)
105 等价转化是探究充要条件的有效途径,但有时利用必要条件解题往往能起到简化求解之功
106 解答应用型问题时,最基本要求是什么?(审题、找准题目中的关键词,设未知数、列出函数关系式、代入初始条件、注明单位、答)
107 解答开放型问题时,需要思维广阔全面,知识纵横联系.如探索性问题先假设存在相应结果,再以此寻找问题成立的充分条件是否存在。对综合分析能力、逻辑思维能力运算能力等要求较高。
108 解答信息型问题时,透彻理解问题中的新信息,这是准确解题的前提。解代数推理问题时,要有较高的逻辑分析能力和推理能力。解答多参型问题时,关键在于恰当地引出参变量,想方设法摆脱参变量的困绕。这当中,参变量的分离、集中、消去、代换以及反客为主等策略,似乎是解答这类问题的通性通法。
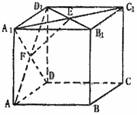
3.(本小题满分14分)
如图(1),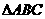 是等腰直角三角形,
是等腰直角三角形,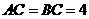 ,
,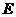 、
、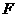 分别为
分别为 、
、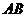 的中点,将
的中点,将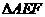 沿
沿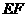 折起, 使
折起, 使 在平面
在平面 上的射影
上的射影 恰为
恰为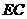 的中点,得到图(2).
的中点,得到图(2).
(Ⅰ)求证: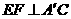 ;
;
(Ⅱ)求三棱锥 的体积.
的体积.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com