10．已知点P在以坐标轴为对称轴的椭圆上，且P到两焦点的距离分别为5、3，过P且与长轴垂直的直线恰过椭圆的一个焦点，求椭圆的方程．

解：法一：设所求的椭圆方程为+＝1(a＞b＞0)或+＝1(a＞b＞0)，

由已知条件得，

a＝4，c＝2，b²＝12.

故所求方程为+＝1或+＝1.

法二：设所求椭圆方程为+＝1(a＞b＞0)或+＝1(a＞b＞0)．

两个焦点分别为F₁，F₂.

由题意知2a＝|PF₁|+|PF₂|＝8，∴a＝4.

在方程+＝1中，令x＝±c得|y|＝，

在方程+＝1中，令y＝±c得|x|＝，

依题意有＝3，∴b²＝12.

∴椭圆的方程为+＝1或+＝1.

9．(2009年高考北京卷)椭圆+＝1的焦点为F₁、F₂，点P在椭圆上，若|PF₁|＝4，则|PF₂|＝________，∠F₁PF₂的大小为________．

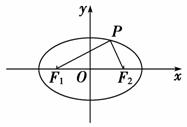解析：∵|PF₁|+|PF₂|＝2a＝6，

∴|PF₂|＝6－|PF₁|＝2.

在△F₁PF₂中，

cos∠F₁PF₂

＝

＝＝－，∴∠F₁PF₂＝120°.

答案：2　120°

8．已知正方形ABCD，则以A、B为焦点，且过C、D两点的椭圆的离心率为________．

解析：设正方形边长为1，则AB＝2c＝1，∴c＝.

∵AC+BC＝1+＝2a，

∴a＝.

∴e＝＝＝－1.

答案：－1

7．F₁、F₂是椭圆+＝1的左、右两焦点，P为椭圆的一个顶点，若△PF₁F₂是等边三角形，则a²＝________.

解析：由题意，因为△PF₁F₂是等边三角形，

故2c＝a，又b＝3，所以a²＝12.

答案：12

6.B₁、B₂是椭圆短轴的两端点，O为椭圆中心，过左焦点F₁作长轴的垂线交椭圆于P，若|F₁B₂|是|OF₁|和|B₁B₂|的等比中项，则的值是(　)

A. 　　　　　　　　B.

C.　 　　　　　　　　D.

解析：选B.设椭圆方程为+＝1(a＞b＞0)，

令x＝－c得y²＝，∴|PF₁|＝，

∴＝＝，

又由|F₁B₂|²＝|OF₁|·|B₁B₂|得a²＝2bc，

∴a⁴＝4b²(a²－b²)．

∴(a²－2b²)²＝0.∴a²＝2b².∴＝.

5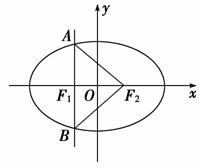．(2010年长沙模拟)已知F₁，F₂分别为椭圆C：+＝1(a＞b＞0)的左，右焦点，过F₁且垂直于x轴的直线交椭圆C于A，B两点，若△ABF₂为钝角三角形，则椭圆C的离心率e的取值范围为(　)

A．(0，－1)　　 　B．(0，－1)

C．(－1,1)　 　　　　D．(－1,1)

解析：选A.由△ABF₂为钝角三角形，得AF₁＞F₁F₂，∴＞2c，化简得c²+2ac－a²＜0，∴e²+2e－1＜0，又0＜e＜1，解得0＜e＜－1，选A.

4．(2009年高考浙江卷)已知椭圆+＝1(a＞b＞0)的左焦点为F，右顶点为A，点B在椭圆上，且BF⊥x轴，直线AB交y轴于点P.若＝2，则椭圆的离心率是(　)

A.　 　　　　　　　　　B.

C.　 　　　　　　　　　　D.

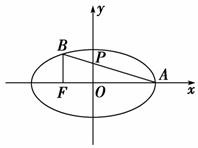解析：选D.如图，由于BF⊥x轴，故x_B＝－c，y_B＝，设P(0，t)，

∵＝2，

∴(－a，t)＝2(－c，－t)．

∴a＝2c，

∴e＝＝.

3．设F₁、F₂为椭圆+y²＝1的左、右焦点，过椭圆中心任作一直线与椭圆交于P、Q两点，当四边形PF₁QF₂面积最大时，·的值等于(　)

A．0　 　　　　　　　B．2

C．4　 　　　　　　　D．－2

解析：选D.易知当P、Q分别在椭圆短轴端点时，四边形PF₁QF₂面积最大．

这时，F₁(－，0)，F₂(，0)，P(0,1)，

∴＝(－，－1)，＝(，－1)，

∴·＝－2.

2．已知椭圆的焦点是F₁、F₂，P是椭圆上的一个动点，如果延长F₁P到Q，使得|PQ|＝|PF₂|，那么动点Q的轨迹是(　)

A．圆　 　　　　　　　B．椭圆

C．双曲线的一支　 　　D．抛物线

解析：选A.∵|PF₁|+|PF₂|＝2a，

|PQ|＝|PF₂|，

∴|PF₁|+|PF₂|＝|PF₁|+|PQ|＝2a.

即|F₁Q|＝2a.

∴动点Q到定点F₁的距离等于定长2a，

故动点Q的轨迹是圆．

1．已知焦点在x轴上的椭圆的离心率为，它的长轴长等于圆C：x²+y²－2x－15＝0的半径，则椭圆的标准方程是(　)

A.+＝1　 　　　　B.+＝1

C.+y²＝1　 　　　　D.+＝1

解析：选A.∵x²+y²－2x－15＝0，

∴(x－1)²+y²＝16，

∴r＝4＝2a，

∴a＝2，

∵e＝，∴c＝1，∴b²＝3.