2．(2009年高考福建卷)一个容量为100的样本，其数据的分组与各组的频数如下：

则样本数据落在(10,40]上的频率为(　)

A．0.13 　　　　　　　　　B．0.39

C．0.52　 　　　　　　　　　D．0.64

解析：选C.由列表知样本数据落在(10,40]上的频数为52，

频率为0.52.

1．如图是某电视台综艺节目举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为(　)

A．84,4.84　　　　　 　B．84,1.6

C．85,4 　　　　　　　　　D．85,1.6

解析：选D.由茎叶图可知评委打出的最低分为79，最高分为93，其余得分为84,84,86,84,87，故平均分为＝85，方差为[3×(84－85)²+(86－85)²+(87－85)²]＝1.6.

12．已知以点C(t，)(t∈R，t≠0)为圆心的圆与x轴交于点O、A，与y轴交于点O、B，其中O为原点．

(1)求证：△OAB的面积为定值；

(2)设直线y＝－2x+4与圆C交于点M，N，若OM＝ON，求圆C的方程．

解：(1)证明：设圆的方程为x²+y²+Dx+Ey＝0，

由于圆心C(t，)，∴D＝－2t，E＝－，

令y＝0得x＝0或x＝－D＝2t，∴A(2t,0)，

令x＝0得y＝0或y＝－E＝，∴B(0，)，

∴S_△OAB＝|OA|·|OB|＝·|2t|·||＝4(定值)．

(2)∵OM＝ON，

∴O在MN的垂直平分线上，而MN的垂直平分线过圆心C, ∴k_OC＝，

∴＝，解得t＝2或t＝－2，

而当t＝－2时，直线与圆C不相交，∴t＝2，

∴D＝－4，E＝－2，

∴圆的方程为x²+y²－4x－2y＝0.

11．圆C通过不同的三点P(k,0)、Q(2,0)、R(0,1)，已知圆C在点P处的切线斜率为1，试求圆C的方程．

解：设圆C的方程为x²+y²+Dx+Ey+F＝0，

则k、2为x²+Dx+F＝0的两根，

∴k+2＝－D,2k＝F，

即D＝－(k+2)，F＝2k，

又圆过R(0,1)，故1+E+F＝0.

∴E＝－2k－1.

故所求圆的方程为

x²+y²－(k+2)x－(2k+1)y+2k＝0，

圆心坐标为(，)．

∵圆C在点P处的切线斜率为1，

∴k_CP＝－1＝，∴k＝－3.∴D＝1，E＝5，F＝－6.

∴所求圆C的方程为x²+y²+x+5y－6＝0.

10．求与x轴相交于A(1,0)和B(5,0)两点且半径为的圆的标准方程．

解：法一：设圆的标准方程为(x－a)²+(y－b)²＝5.

∵点A，B在圆上，所以可得到方程组：

，解得a＝3，b＝±1.

∴圆的标准方程是(x－3)²+(y－1)²＝5或(x－3)²+(y+1)²＝5.

法二：由A、B两点在圆上可知线段AB是圆的一条弦，根据平面几何知识：这个圆的圆心在线段AB的垂直平分线x＝3上，于是可设圆心为C(3，b)，又|AC|＝，即＝，解得b＝1或b＝－1.

因此，所求圆的标准方程为(x－3)²+(y－1)²＝5或(x－3)²+(y+1)²＝5.

9．一个等腰三角形底边上的高等于4，底边两端点的坐标是(－3,0)，(3,0)，则它的外接圆方程是________．

解析：底边端点关于原点对称，

所以底边的中垂线方程为x＝0，①

底边上的高等于4，说明第三个顶点的坐标为(0,4)或(0，－4)．

一腰的中垂线方程为y－2＝(x－)或y+2＝－(x－)，②

方程①②联立得圆心坐标为(0，)或(0，－)，

半径为＝，

所求圆的方程为x²+(y+)²＝或x²+(y－)²＝.

答案：x²+(y+)²＝或x²+(y－)²＝

8.圆心在原点且圆周被直线3x+4y+15＝0分成1∶2两部分的圆的方程为________．

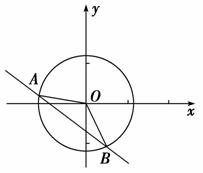解析：如图，因为圆周被直线3x+4y+15＝0分成1∶2两部分，所以∠AOB＝120°.而圆心到直线3x+4y+15＝0的距离d＝＝3，在△AOB中，可求得OA＝6.所以所求圆的方程为x²+y²＝36.

答案：x²+y²＝36

7．如果圆的方程为x²+y²+kx+2y+k²＝0.那么当圆面积最大时，圆心为________．

解析：将方程配方，得(x+)²+(y+1)²＝－k²+1.

∴r²＝1－k²>0，r_max＝1，此时k＝0.

∴圆心为(0，－1)．

答案：(0，－1)

6．一束光线从点A(－1,1)出发经x轴反射到圆C：(x－2)²+(y－3)²＝1上的最短路程是(　)

A．4　 　　　　　　　B．5

C．3－1　 　　　　　D．2

解析：选A.圆C的圆心C的坐标为(2,3)，半径r＝1.点A(－1,1)关于x轴的对称点A′的坐标为(－1，－1)．因A′在反射线上，所以最短距离为|A′C|－r，即－1＝4.

5．(2008年高考山东卷)若圆C的半径为1，圆心在第一象限，且与直线4x－3y＝0和x轴都相切，则该圆的标准方程是(　)

A．(x－3)²+(y－)²＝1 　　　　　B．(x－2)²+(y－1)²＝1

C．(x－1)²+(y－3)²＝1　 　　　　D．(x－)²+(y－1)²＝1

解析：选B.设圆心坐标为(a，b)，则，又b>0，故b＝1，由|4a－3|＝5得a＝2或a＝－，又a>0，故a＝2，所求圆的标准方程是(x－2)²+(y－1)²＝1.(采用检验的方法也可以)