3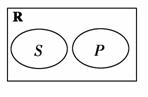．(2010年上海市十四校高三联考)设全集为实数集R，已知非空集合S，P相互关系如图所示，其中

S＝{x|x>10－a²}，

P＝{x|5－2a<x<3a}，

则实数a的取值范围是(　)

A．－5<a<2　 　　　　　　　　B．1<a<2

C．1<a≤2　 　　　　　　　　　D．－5≤a≤2

解析：选C.由题图可知，S∩P＝∅，S≠∅，P≠∅，从而∴1<a≤2.故选C.

2．(2009年高考山东卷)在R上定义运算⊙：a⊙b＝ab+2a+b，则满足x⊙(x－2)<0的实数x的取值范围为(　)

A．(0,2)　 　　　　　　　　　B．(－2,1)

C．(－∞，－2)∪(1，+∞)　 　D．(－1,2)

解析：选B.∵x⊙(x－2)＝x(x－2)+2x+x－2<0，

∴x²+x－2<0.∴－2<x<1.

1．(原创题)不等式x²+ax+4<0的解集不是空集，则实数a的取值范围是(　)

A．－4≤a≤4　 　　　　　　　B．－4<a<4

C．a≥4或a≤－4　 　　　　　D．a<－4或a>4

解析：选D.x²+ax+4<0的解集不是空集，只需Δ＝a²－16>0，∴a<－4或a>4，故选D.

12．(2009年高考宁夏、海南卷)某工厂有工人1000名，其中250名工人参加过短期培训(称为A类工人)，另外750名工人参加过长期培训(称为B类工人)．现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人，调查他们的生产能力(此处生产能力指一天加工的零件数)．

(1)求甲、乙两工人都被抽到的概率，其中甲为A类工人，乙为B类工人；

(2)从A类工人中的抽查结果和从B类工人中的抽查结果分别如下表1和表2.

表1：

表2：

①先确定x、y，再完成频率分布直方图，就生产能力而言，A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小？(不用计算，可通过观察直方图直接回答结论)

②分别估计A类工人和B类工人生产能力的平均数，并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表)．

解：(1)甲、乙被抽到的概率均为，且事件“甲工人被抽到”与事件“乙工人被抽到”相互独立，故甲、乙两工人都被抽到的概率为P＝×＝.

(2)①由题意知A类工人中应抽查25名，B类工人中应抽查75名．

故4+8+x+5+3＝25，得x＝5，

6+y+36+18＝75，得y＝15.

频率分布直方图如下：

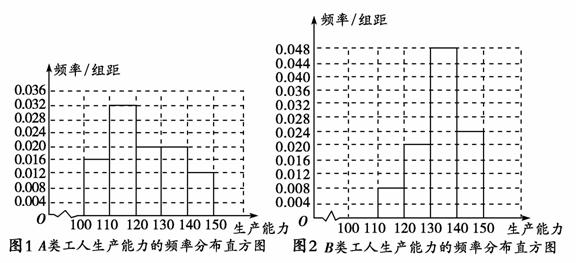
从直方图可以判断：B类工人中个体间的差异程度更小．

②_A＝×105+×115+×125

+×135+×145＝123，

_B＝×115+×125+×135+×145＝133.8，

＝×123+×133.8＝131.1.

A类工人生产能力的平均数、B类工人生产能力的平均数以及全厂工人生产能力的平均数的估计值分别为123,133.8和131.1.

11．(2009年高考安徽卷)某良种培育基地正在培育一种小麦新品种A.将其与原有的一个优良品种B进行对照试验．两种小麦各种植了25亩，所得亩产数据(单位：千克)如下：

品种A：

357,359,367,368,375,388,392,399,400,405,412,414,415,421,423,423,427,430,430,434,443,445,445,451,454

品种B：

363,371,374,383,385,386,391,392,394,394,395,397,397,400,401,401,403,406,407,410,412,415,416,422,430

(1)画出茎叶图；

(2)用茎叶图处理现有的数据，有什么优点？

(3)通过观察茎叶图，对品种A与B的亩产量及其稳定性进行比较，写出统计结论．

解：(1)

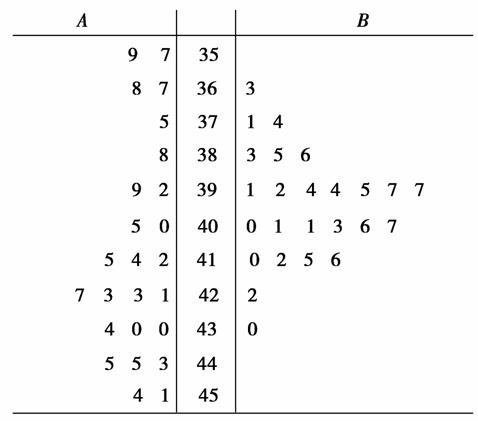
(2)由于每个品种的数据都只有25个，样本不大，画茎叶图很方便；此时茎叶图不仅清晰明了地展示了数据的分布情况，便于比较，没有任何信息损失，而且还可以随时记录新的数据．

(3)通过观察茎叶图可以看出：①品种A的亩产平均数(或均值)比品种B高；②品种A的亩产标准差(或方差)比品种B大，故品种A的亩产稳定性较差．

10．某工厂人员及工资构成如表：

(1)指出这个问题中工资的众数、中位数、平均数；

(2)这个问题中，平均数能客观地反映该工厂的工资水平吗？为什么？

解：(1)众数200，中位数220，平均数

＝

＝300.

(2)平均数受数据中的极端值的影响较大，这个平均数是从一名工资极高(是工人工资的11倍)的经理和其他四类员工的周工资计算出来的，它不能客观地反映该工厂的工资水平．

9．已知总体的各个体的值由小到大依次为2,3,3,7，a，b,12，13.7，18.3,20，且总体的中位数为10.5，平均数为10.若要使该总体的方差最小，则a、b的取值分别是________．

解析：这10个数的中位数为＝10.5.

这10个数的平均数为10.

要使总体方差最小，

即(a－10)²+(b－10)²最小．

又∵(a－10)²+(b－10)²＝(21－b－10)²+(b－10)²

＝(11－b)²+(b－10)²＝2b²－42b+221，

∴当b＝10.5时，(a－10)²+(b－10)²取得最小值．

又∵a+b＝21，

∴a＝10.5，b＝10.5.

答案：a＝10.5，b＝10.5

8．(2009年高考辽宁卷)某企业3个分厂生产同一种电子产品，第一、二、三分厂的产量之比为1∶2∶1，用分层抽样方法(每个分厂的产品为一层)从3个分厂生产的电子产品中共抽取100件作使用寿命的测试，由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为980 h,1020 h,1032 h，则抽取的100件产品的使用寿命的平均值为________h.

解析：由于三个厂的产量比为1∶2∶1　　 ，所以从三个厂抽出产品比例也应为1∶2∶1.所以100件产品的使用寿命平均值为＝1013.

答案：1013

7．如图所示是一个容量为200的样本的频率分布直方图，请根据图形中的数据填空：

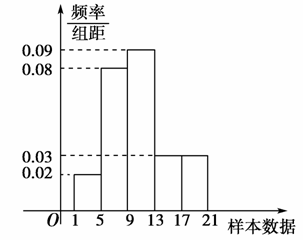
(1)样本数据落在[5,9)内的频率是　　；

(2)样本数据落在[9,13)内的频数是　　.

解析：该题考查频率分布直方图的意义及应用图形解题的能力．频率＝×组距＝0.08×4＝0.32，频数＝频率×样本容量＝0.09×4×200＝72.

答案：0.32　72

4．4-4.5之间的频数为100×0.1×0.3＝3.

根据前4组频数成等比数列，则4.6-4.7之间的频数为1·()³＝27.∴最大频率a＝＝0.27.

根据后6组频数成等差数列，且有100－13＝87(人)，设公差为d，则6×27+d＝87，∴d＝－5，所以b＝4×27+×(－5)＝78.