
题目列表(包括答案和解析)
50.已知椭圆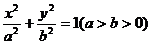 的右准线
的右准线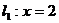 与
与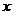 轴相交于点
轴相交于点 ,右焦点
,右焦点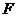 到上顶点的距离为
到上顶点的距离为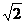 ,点
,点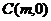 是线段
是线段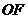 上的一个动点.
上的一个动点.
(1)求椭圆的方程;
(2)是否存在过点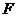 且与
且与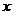 轴不垂直的直线
轴不垂直的直线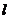 与椭圆交于
与椭圆交于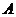 、
、 两点,使得
两点,使得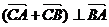 ,并说明理由.
,并说明理由.
解 (1)由题意可知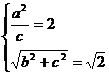 ,又
,又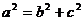 ,解得
,解得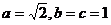 ,
,
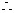 椭圆的方程为
椭圆的方程为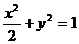 ;
;
(2)由(1)得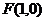 ,所以
,所以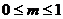 .假设存在满足题意的直线
.假设存在满足题意的直线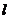 ,设
,设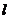 的方程为
的方程为
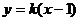 ,代入
,代入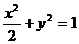 ,得
,得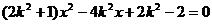 ,
,
设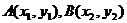 ,则
,则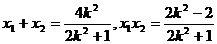 ①
①
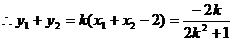 ,
,
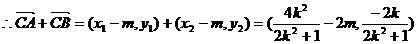 ,
,
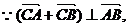 而
而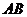 的方向向量为
的方向向量为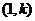 ,
,
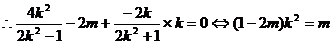 ;
;
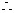 当
当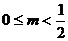 时,
时,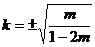 ,即存在这样的直线
,即存在这样的直线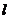 ;
;
当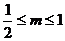 时,
时,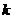 不存在,即不存在这样的直线
不存在,即不存在这样的直线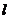 .
.
49.设函数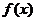 的定义域与值域均为R,
的定义域与值域均为R,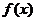 的反函数为
的反函数为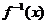 ,定义数列{
,定义数列{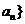 中,
中,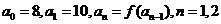 ,……。
,……。
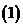 若对于任意实数x,均有
若对于任意实数x,均有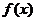 +
+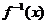 =2.5x,求证:①
=2.5x,求证:①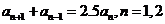 ,……。
,……。
②设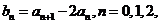 ……,求{
……,求{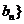 的通项公式。
的通项公式。
 若对于任意实数x,均有
若对于任意实数x,均有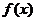 +
+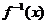 <2.5x,是否存在常数A、B同时满足:
<2.5x,是否存在常数A、B同时满足:
①当n=0.or.n=1时,有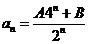 成立;②当n=2、3、4、……,时,
成立;②当n=2、3、4、……,时,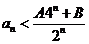 成立。
成立。
如果存在,求出A、B的值;如果不存在,说明理由。
解:(1)由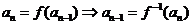 ,又在等式
,又在等式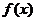 +
+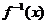 =2.5x中令
=2.5x中令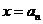 ,
,
从而有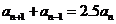 ………………(1)成立。
………………(1)成立。
又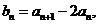 及(1)式有:
及(1)式有: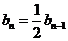 ,所以{
,所以{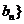
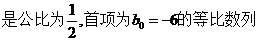 ,
,
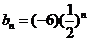 。
。
(2)由n=0.or.n=1时,有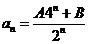 成立,可求得A=B=4,
成立,可求得A=B=4,
由对于任意实数x,均有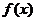 +
+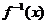 <2.5x,可得
<2.5x,可得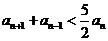 ………………(2)
………………(2)
下面利用(2)和A=B=4,用数学归纳法证明:
当n=2、3、4、……,时,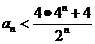 成立即可,证明过程容易,略去。
成立即可,证明过程容易,略去。
所以存在实数A=B=4,使结论成立。
48.已知函数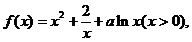
(1) 若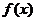 在
在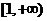 上单调递增,求
上单调递增,求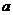 的取值范围;
的取值范围;
(2) 若定义在区间D上的函数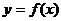 对于区间D上的任意两个值
对于区间D上的任意两个值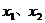 总有以下不等式
总有以下不等式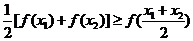 成立,则称函数
成立,则称函数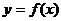 为区间D上的“凹函数”.
为区间D上的“凹函数”.
试判断当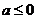 时,
时,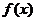 是否为“凹函数”,并对你的判断加以证明.
是否为“凹函数”,并对你的判断加以证明.
解:(Ⅰ)由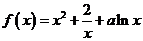 ,得
,得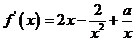 ……………………2分
……………………2分
欲使函数为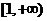 上单调增函数,则
上单调增函数,则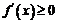 在
在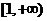 上恒成立,即不等式
上恒成立,即不等式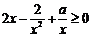 在
在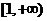 上恒成立.也即
上恒成立.也即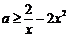 在
在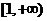 上恒成立.………………4分
上恒成立.………………4分
令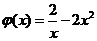 ,上述问题等价于
,上述问题等价于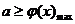 ,而
,而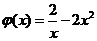 为在
为在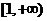 上的减函数,则
上的减函数,则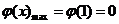 ,于是
,于是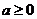 为所求. ………………………………………………6分
为所求. ………………………………………………6分
(Ⅱ)证明:由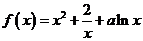 得
得
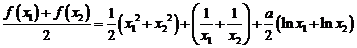
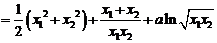 ………………………………7分
………………………………7分
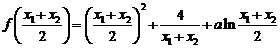 ………………………………………8分
………………………………………8分
而 ① ………………………10分
① ………………………10分
又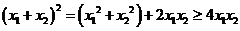 , ∴
, ∴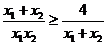 ② …………11分
② …………11分
∵ ∴
∴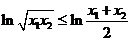 ,
,
∵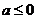 ∴
∴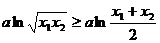 ③ …………………………………13分
③ …………………………………13分
由①、②、③得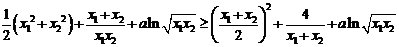
即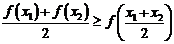 ,
,
从而由凹函数的定义可知函数为凹函数. …………14分
46.已知集合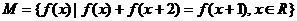 ,
, 。
。
(1)判断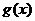 与
与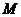 的关系,并说明理由;
的关系,并说明理由;
(2)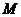 中的元素是否都是周期函数,证明你的结论;
中的元素是否都是周期函数,证明你的结论;
(3)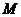 中的元素是否都是奇函数,证明你的结论。
中的元素是否都是奇函数,证明你的结论。
解(1)∵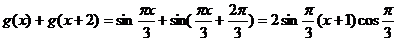
=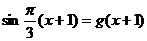 ∴
∴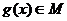 ……6分
……6分
(2)因 是周期为6的周期函数,猜测
是周期为6的周期函数,猜测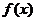 也是周期为6的周期函数
也是周期为6的周期函数
由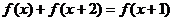 ,得
,得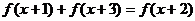 ,
,
∴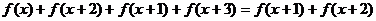
∴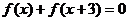 , ∴
, ∴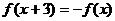 ,
,
∴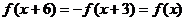 ,得证
,得证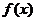 是周期为6的周期函数,
是周期为6的周期函数,
故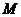 中的元素都是周期为6的周期函数。……12分
中的元素都是周期为6的周期函数。……12分
(3)令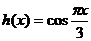 ,可证得
,可证得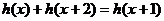 ……16分
……16分
∴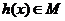 ,但
,但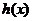 是偶函数,不是奇函数,
是偶函数,不是奇函数,
∴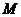 中的元素不都是奇函数。…
中的元素不都是奇函数。…
47设函数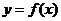 的定义域为R,当
的定义域为R,当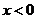 时,
时, ,且对任意的实数
,且对任意的实数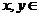 R,有
R,有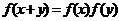 成立
成立 数列
数列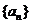 满足
满足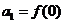 ,且
,且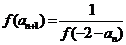 (
(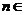 N)
N)
(1)证明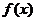 在R上为减函数;
在R上为减函数;
(2)求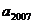 的值;
的值;
(3)若不等式 对一切
对一切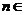 N均成立,求
N均成立,求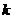 的最大值
的最大值
解:(1)令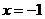 ,
,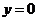 ,得
,得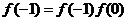 ,
,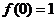 ,故
,故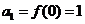

当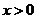 时,
时,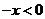 ,
,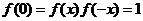 ,进而得
,进而得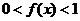

设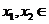 R,且
R,且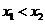 ,
,
则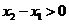 ,
,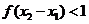 ,
,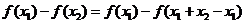
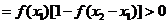

故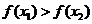 ,函数
,函数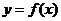 在R上是单调递减函数
在R上是单调递减函数
(2)由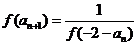 ,得
,得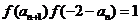

故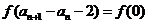 ,
,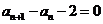 ,
,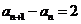 (
(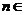 N)
N)
因此,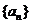 是首项为1,公差为2的等差数列
是首项为1,公差为2的等差数列 由此得
由此得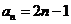 ,
, 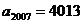

(3) 由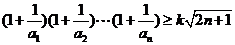 恒成立,
恒成立,
知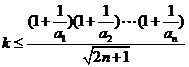 恒成立
恒成立
设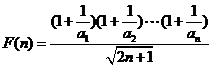 ,则
,则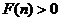 ,
,
且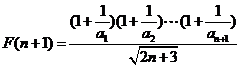

又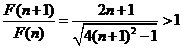 ,即
,即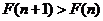 ,故
,故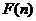 为关于
为关于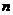 的单调增函数,
的单调增函数,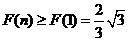
 所以,
所以,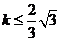 ,即
,即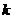 的最大值为
的最大值为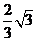

43.设数列{an}的各项都是正数,且对任意n∈N+,都有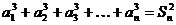 ,记Sn为数列{an}的前n项和.
,记Sn为数列{an}的前n项和.
(1)求证: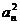 =2Sn-an;
=2Sn-an;
(2)求数列{an}的通项公式;
(3)若 (
(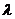 为非零常数,n∈N+),问是否存在整数
为非零常数,n∈N+),问是否存在整数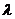 ,使得对任意 n∈N+,都有bn+1>bn.
,使得对任意 n∈N+,都有bn+1>bn.
解:(1)在已知式中,当n=1时,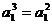
∵a1>0 ∴a1=1……………………………………1分
当n≥2时,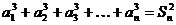 ①
①
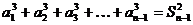 ②
②
①-②得,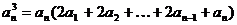 …………………………3分
…………………………3分
∵an>0 ∴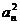 =2a1+2a2+…+2an-1+an,
=2a1+2a2+…+2an-1+an,
即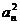 =2Sn-an ∵a1=1适合上式
=2Sn-an ∵a1=1适合上式
∴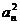 =2Sn-an(n∈N+)……………………5分
=2Sn-an(n∈N+)……………………5分
(2)由(1)知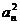 =2Sn-an(∈N+) ③
=2Sn-an(∈N+) ③
当n≥2时, 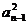 =2Sn-1-an-1 ④
=2Sn-1-an-1 ④
③-④得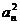 -
-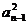 =2(Sn-Sn-1)-an+an-1=2an-an+ an-1= an+
an-1
=2(Sn-Sn-1)-an+an-1=2an-an+ an-1= an+
an-1
∵an+an-1>0 ∴an-an-1=1……………………8分
∴数列{an}是等差数列,首项为1,公差为1,可得an=n………………9分
(3)∵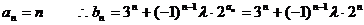
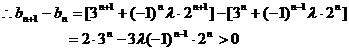
∴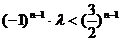 ⑤……………………11分
⑤……………………11分
当n=2k-1,k=1,2,3,……时,⑤式即为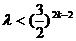 ⑥
⑥
依题意,⑥式对k=1,2,3……都成立,∴λ<1………………12分
当n=2k,k=1,2,3,…时,⑤式即为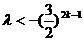 ⑦
⑦
依题意,⑦式对k=1,2,3,……都成立,
∴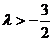 ……………………13分
……………………13分
∴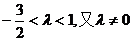
∴存在整数λ=-1,使得对任意n∈N,都有bn+1>bn……………
44设关于x的方程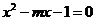 有两个实根
有两个实根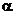 、
、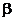 ,且
,且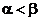 .定义函数
.定义函数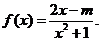
(Ⅰ)求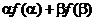 的值;
的值;
(Ⅱ)判断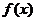 在区间
在区间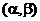 上的单调性,并加以证明;
上的单调性,并加以证明;
(Ⅲ)若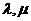 为正实数,证明不等式:
为正实数,证明不等式: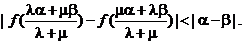
(Ⅰ)解:∵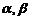 是方程
是方程 的两个实根
的两个实根
∴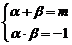
∴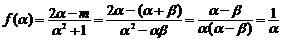
同理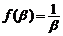
∴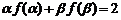 …………3分
…………3分
(Ⅱ)∵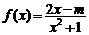
∴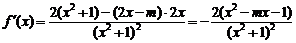 …………4分
…………4分
当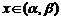 时,
时,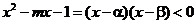 …………5分
…………5分
而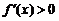
∴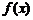 在
在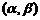 上为增函数
…………7分
上为增函数
…………7分
(Ⅲ)∵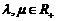 且
且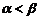
∴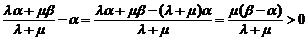
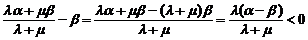
∴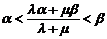 …………9分
…………9分
由(Ⅱ)可知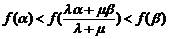
同理可得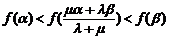 …………10分
…………10分
∴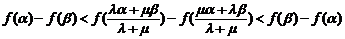
∴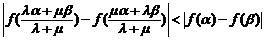 …………12分
…………12分
又由(Ⅰ)知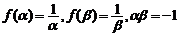
∴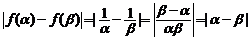
所以 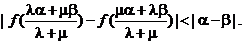 ………
………
45已知数列{a n}前n项的和为S n,前n项的积为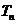 ,且满足
,且满足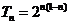 。
。
①求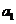 ;
②求证:数列{a n}是等比数列;
;
②求证:数列{a n}是等比数列;
③是否存在常数a,使得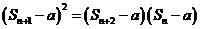 对
对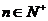 都成立?
都成立?
若存在,求出a,若不存在,说明理由。
解、①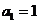 ;③
;③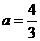
42.已知函数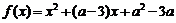 (a为常数).
(a为常数).
(1)如果对任意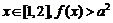 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(2)设实数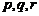 满足:
满足: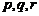 中的某一个数恰好等于a,且另两个恰为方程
中的某一个数恰好等于a,且另两个恰为方程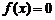 的两实根,判断①
的两实根,判断①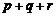 ,②
,②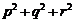 ,③
,③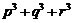 是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数
是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数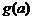 ,并求
,并求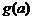 的最小值;
的最小值;
(3)对于(2)中的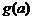 ,设
,设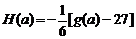 ,数列
,数列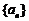 满足
满足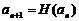
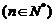 ,且
,且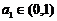 ,试判断
,试判断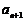 与
与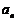 的大小,并证明.
的大小,并证明.
解:(1)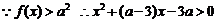
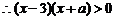 对
对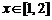 恒成立,
恒成立,
又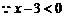 恒成立,
恒成立,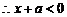 对
对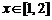 恒成立,
恒成立,
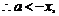 又
又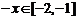 ,
,
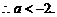
(2)由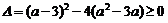 得:
得: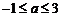 ,
,
不妨设 ,则q,r恰为方程两根,由韦达定理得:
,则q,r恰为方程两根,由韦达定理得:
①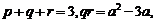
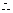 ②
②
③而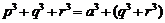
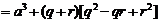
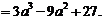
设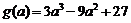 ,求导得:
,求导得: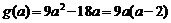
当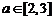 时,
时,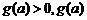 递增;当
递增;当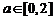 时,
时,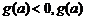 递减;
递减;
当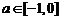 时,
时,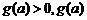 递增,
递增,
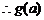 在
在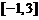 上的最小值为
上的最小值为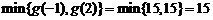
(3)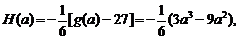
如果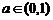 ,则
,则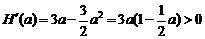
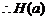 在
在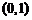 为递增函数,
为递增函数,
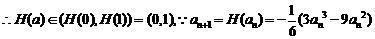
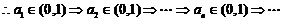
又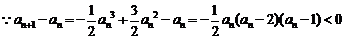
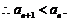
41.数列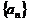 ,
,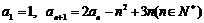
⑴是否存在常数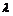 、
、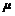 ,使得数列
,使得数列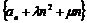 是等比数列,若存在,求出
是等比数列,若存在,求出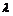 、
、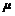 的值,若不存在,说明理由。
的值,若不存在,说明理由。
⑵设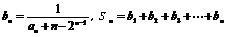 ,证明:当
,证明:当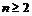 时,
时,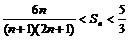 .
.
⑴解:设 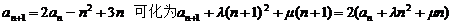 ,
,
即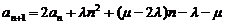 …………………………… (2分)
…………………………… (2分)
故 …………………………… (4分)
…………………………… (4分)
∴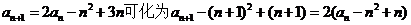 ………(5分)
………(5分)
又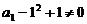 ……………………………………………………………………(6分)
……………………………………………………………………(6分)
故存在 是等比数列 ……………(7分)
是等比数列 ……………(7分)
⑵证明:由⑴得 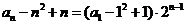 ∴
∴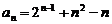 ,
,
故 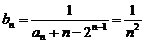 ……………………………………………… (8分)
……………………………………………… (8分)
∵ 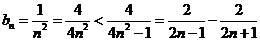 ………………………… (9分)
………………………… (9分)
∴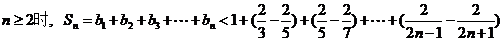
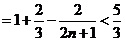 ……………………………………(11分)
……………………………………(11分)
现证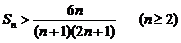 .
.
当
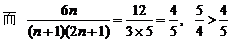 ,
,
故 时不等式成立 ………………………………………………(12分)
时不等式成立 ………………………………………………(12分)
当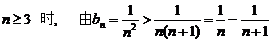 得
得
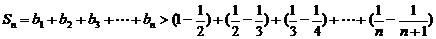
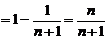 ,且由
,且由 ,
,
∴ ……………………………………
(14分)
……………………………………
(14分)
4.若函数f(x)=则f(-)的值为________.
解析:由已知得:f(-)=f(-)+1=f()+2=-cos+2=.
3.(2008年高考浙江卷)若cosα+2sinα=-,则tanα=( )
A. B.2
C.- D.-2
解析:选B.由
将①代入②得(sinα+2)2=0,
∴sinα=-,cosα=-.故选B.
2.(2009年高考陕西卷)若tanα=2,则的值为( )
A.0 B.
C.1 D.
解析:选B.===.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com