
题目列表(包括答案和解析)
1.配方法--二次函数(二次函数在给出区间上的最值有两类:一是求闭区间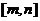 上的最值;二是求区间定(动),对称轴动(定)的最值问题。求二次函数的最值问题,勿忘数形结合,注意“两看”:一看开口方向;二看对称轴与所给区间的相对位置关系),如
上的最值;二是求区间定(动),对称轴动(定)的最值问题。求二次函数的最值问题,勿忘数形结合,注意“两看”:一看开口方向;二看对称轴与所给区间的相对位置关系),如
(1)求函数 的值域
的值域
(答:[4,8]);
(2)当 时,函数
时,函数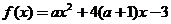 在
在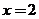 时取得最大值,则
时取得最大值,则 的取值范围是___
的取值范围是___
(答: );
);
(3)已知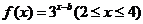 的图象过点(2,1),则
的图象过点(2,1),则 的值域为______
的值域为______
(答:[2, 5])
3.复合函数的定义域:若已知 的定义域为
的定义域为 ,其复合函数
,其复合函数 的定义域由不等式
的定义域由不等式 解出即可;若已知
解出即可;若已知 的定义域为
的定义域为 ,求
,求 的定义域,相当于当
的定义域,相当于当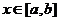 时,求
时,求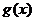 的值域(即
的值域(即 的定义域)。如
的定义域)。如
(1)若函数 的定义域为
的定义域为 ,则
,则 的定义域为__________
的定义域为__________
(答: );
);
(2)若函数 的定义域为
的定义域为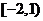 ,则函数
,则函数 的定义域为________
的定义域为________
(答:[1,5]).
2.根据实际问题的要求确定自变量的范围。
1.根据解析式要求如偶次根式的被开方大于零,分母不能为零,对数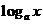 中
中 且
且 ,三角形中
,三角形中 , 最大角
, 最大角 ,最小角
,最小角 等。如
等。如
(1)函数 的定义域是____
的定义域是____
(答: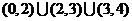 );
);
(2)若函数 的定义域为R,则
的定义域为R,则 _______
_______
(答: );
);
(3)函数 的定义域是
的定义域是 ,
, ,则函数
,则函数 的定义域是__________
的定义域是__________
(答: );
);
(4)设函数 ,①若
,①若 的定义域是R,求实数
的定义域是R,求实数 的取值范围;②若
的取值范围;②若 的值域是R,求实数
的值域是R,求实数 的取值范围
的取值范围
(答:① ;②
;②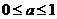 )
)
若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“天一函数”,那么解析式为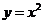 ,值域为{4,1}的“天一函数”共有______个
,值域为{4,1}的“天一函数”共有______个
(答:9)
(1)已知函数 ,
,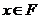 ,那么集合
,那么集合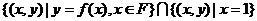 中所含元素的个数有 个
中所含元素的个数有 个
(答: 0或1);
(2)若函数 的定义域、值域都是闭区间
的定义域、值域都是闭区间 ,则
,则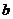 =
=
(答:2)
㈠中元素必须都有象且唯一;㈡B中元素不一定都有原象,但原象不一定唯一。如:
(1)设 是集合
是集合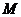 到
到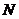 的映射,下列说法正确的是
的映射,下列说法正确的是
A、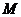 中每一个元素在
中每一个元素在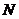 中必有象
中必有象
B、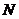 中每一个元素在
中每一个元素在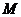 中必有原象
中必有原象
C、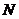 中每一个元素在
中每一个元素在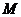 中的原象是唯一的
中的原象是唯一的
D、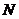 是
是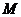 中所在元素的象的集合
中所在元素的象的集合
(答:A);
(2)点 在映射
在映射 的作用下的象是
的作用下的象是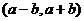 ,则在
,则在 作用下点
作用下点 的原象为点________
的原象为点________
(答:(2,-1));
(3)若 ,
,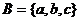 ,
, ,则
,则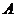 到
到 的映射有 个,
的映射有 个, 到
到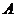 的映射有 个,
的映射有 个,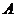 到
到 的函数有 个
的函数有 个
(答:81,64,81);
(4)设集合 ,映射
,映射 满足条件“对任意的
满足条件“对任意的 ,
, 是奇数”,这样的映射
是奇数”,这样的映射 有____个
有____个
(答:12);
(5)设 是集合A到集合B的映射,若B={1,2},则
是集合A到集合B的映射,若B={1,2},则 一定是_____
一定是_____
(答: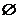 或{1}).
或{1}).
以抛物线定义为例,若点 在抛物线
在抛物线
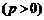 或
或 上,则定义式
上,则定义式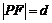 可分别变式为
可分别变式为 或
或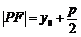 ,等等.
,等等.
例3 (全国卷Ⅱ.文)抛物线 上一点
上一点 的纵坐标为4,则点
的纵坐标为4,则点 与抛物线焦点的距离为( )
与抛物线焦点的距离为( )
A.2 B.3 C.4 D.5
解:已知抛物线 ,得
,得 ,
,
 根据抛物线的定义可知
根据抛物线的定义可知 ,故选D.
,故选D.
点评:变用定义,实现了距离与坐标之间的转化.
以双曲线定义为例,若点P的轨迹是双曲线,则等式 恒成立.
恒成立.
例2 (福建卷)已知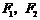 是双曲线
是双曲线 的两焦点,以线段
的两焦点,以线段 为边作正三角形
为边作正三角形 ,若边
,若边 的中点在双曲线上,则双曲线的离心率是( )
的中点在双曲线上,则双曲线的离心率是( )
A.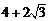 B.
B.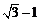 C.
C.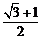 D.
D.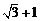
解: 是正三角形且边
是正三角形且边 的中点在双曲线上,则设边
的中点在双曲线上,则设边 的中点为
的中点为 ,有
,有 ,
, ,从而
,从而 ,
, .
.
 根据双曲线的定义可知
根据双曲线的定义可知 ,
,
解得 ,故选D.
,故选D.
点评:当已知是何种圆锥曲线且与两焦点有关时,可直接利用定义求解,以达到简缩思路、简化运算的目的.
以椭圆定义为例,若 ,则点
,则点 的轨迹必是椭圆.
的轨迹必是椭圆.
例1 (重庆卷.文)已知点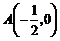 ,点
,点 是圆
是圆 (
(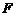 为圆心)上一动点,线段
为圆心)上一动点,线段 的垂直平分线交
的垂直平分线交 于
于 ,则动点
,则动点 的轨迹方程是 .
的轨迹方程是 .
解:由已知圆知圆心 ,半径
,半径 .
.
 线段
线段 的垂直平分线交
的垂直平分线交 于
于 ,
,
 ,
,
从而 ,且
,且 ,
,
根据椭圆的定义可知动点 的轨迹为椭圆,
的轨迹为椭圆,
且 ,
,
又由条件可知焦点在 轴上,
轴上,
故所求点 的轨迹方程为
的轨迹方程为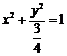 .
.
点评:由已知点A与圆心F的对称性,可以猜测A,F是椭圆或双曲线的两焦点,一举奠定了利用定义求轨迹方程的基础.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com