
题目列表(包括答案和解析)
8.(天津市武清区2009-2010学年高三下学期第一次模拟文)在空间四边形ABCD中,E、F分别为AC、BD的中点,若CD=2AB=4,EF⊥AB,则EF与CD所成的角为( D )
A.900 B.600
C.450 D.300
5.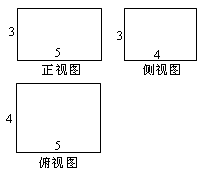 (天津市武清区2009-2010学年高三下学期第一次模拟理)一个几何体的三视图如图所示,它的一条对角线
(天津市武清区2009-2010学年高三下学期第一次模拟理)一个几何体的三视图如图所示,它的一条对角线
的两个端点为A、B,则经过这个几何体的面,A、B间的最短路程是( B )
A.5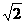 B.
B.
C.4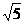 D.3
D.3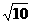
(1)设函数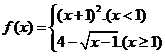 ,则使得
,则使得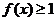 的自变量
的自变量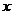 的取值范围是__
的取值范围是__
(答: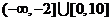 );
);
(2)已知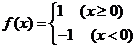 ,则不等式
,则不等式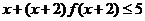 的解集_____
的解集_____
(答: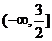 )
)
8.导数法--一般适用于高次多项式函数,如
求函数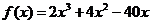 ,
,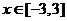 的最小值。
的最小值。
(答:-48)
提醒:(1)求函数的定义域、值域时,你按要求写成集合形式了吗?
(2)函数的最值与值域之间有何关系?
7.不等式法--利用基本不等式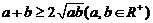 求函数的最值,其题型特征解析式是和式时要求积为定值,解析式是积时要求和为定值,不过有时须要用到拆项、添项和两边平方等技巧。如
求函数的最值,其题型特征解析式是和式时要求积为定值,解析式是积时要求和为定值,不过有时须要用到拆项、添项和两边平方等技巧。如
设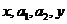 成等差数列,
成等差数列,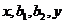 成等比数列,则
成等比数列,则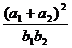 的取值范围是__.
的取值范围是__.
(答: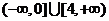 )。
)。
6.判别式法--对分式函数(分子或分母中有一个是二次)都可通用,但这类题型有时也可以用其它方法进行求解,不必拘泥在判别式法上,也可先通过部分分式后,再利用均值不等式:
①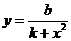 型,可直接用不等式性质,如
型,可直接用不等式性质,如
求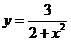 的值域
的值域
(答: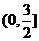 )
)
② 型,先化简,再用均值不等式,如
型,先化简,再用均值不等式,如
(1)求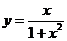 的值域
的值域
(答: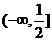 );
);
(2)求函数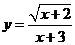 的值域
的值域
(答: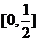 )
)
③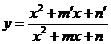 型,通常用判别式法;如
型,通常用判别式法;如
已知函数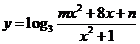 的定义域为R,值域为[0,2],求常数
的定义域为R,值域为[0,2],求常数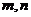 的值
的值
(答: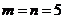 )
)
④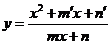 型,可用判别式法或均值不等式法,如
型,可用判别式法或均值不等式法,如
求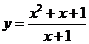 的值域
的值域
(答: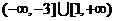 )
)
5.数形结合法--函数解析式具有明显的某种几何意义,如两点的距离、直线斜率、等等,如
(1)已知点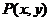 在圆
在圆 上,求
上,求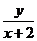 及
及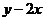 的取值范围
的取值范围
(答: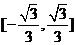 、
、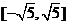 );
);
(2)求函数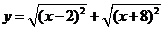 的值域
的值域
(答: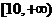 );
);
(3)求函数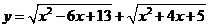 及
及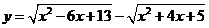 的值域
的值域
(答: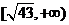 、
、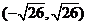 )
)
注意:求两点距离之和时,要将函数式变形,使两定点在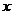 轴的两侧,而求两点距离之差时,则要使两定点在
轴的两侧,而求两点距离之差时,则要使两定点在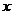 轴的同侧。
轴的同侧。
4.单调性法--利用一次函数,反比例函数,指数函数,对数函数等函数的单调性,如
求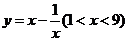 ,
, ,
,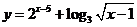 的值域
的值域
(答: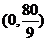 、
、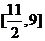 、
、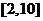 );
);
3.函数有界性法--直接求函数的值域困难时,可以利用已学过函数的有界性,来确定所求函数的值域,最常用的就是三角函数的有界性,如
求函数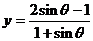 ,
,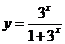 ,
,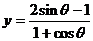 的值域
的值域
(答: 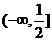 、(0,1)、
、(0,1)、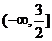 );
);
2.换元法--通过换元把一个较复杂的函数变为简单易求值域的函数,其函数特征是函数解析式含有根式或三角函数公式模型,如
(1) 的值域为_____
的值域为_____
(答: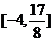 );
);
(2)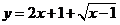 的值域为_____
的值域为_____
(答: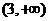 )
)
(3)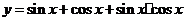 的值域为____
的值域为____
(答: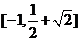 );
);
(4)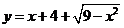 的值域为____
的值域为____
(答: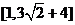 );
);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com