
题目列表(包括答案和解析)
22、解:(1)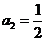 ,
, 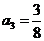 ,
,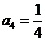 ……………………(2分)
……………………(2分)
由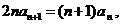 得
得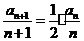 ……………………(3分)
……………………(3分)
即数列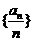 是以
是以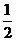 为首项,以
为首项,以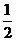 为公比的等比数列
为公比的等比数列
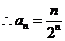 ……………………(4分)
……………………(4分)
注:用数学归纳法也可以。
(2)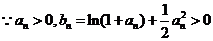
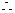 要证明
要证明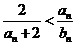 只需证明
只需证明
即证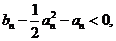 即证明
即证明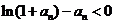 成立……………………(6分)
成立……………………(6分)
构造函数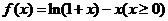 ……………………(7分)
……………………(7分)
则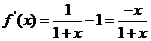 ,……………………(8分)
,……………………(8分)
当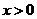 时,
时, ,即
,即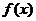 在
在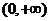 上单调递减,所以
上单调递减,所以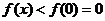
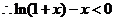 ,即
,即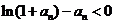 对一切
对一切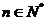 都成立,
都成立,
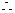
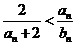 ……………………(10分)
……………………(10分)
(3)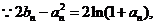
由(2)可知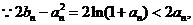
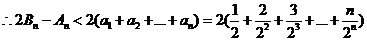 ……………………(12分)
……………………(12分)
利用错位相减法求得
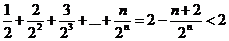
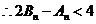 ……………………(14分)
……………………(14分)
22.(天津市天津一中2010届高三第四次月考理科)设数列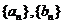 满足
满足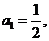
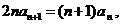 且
且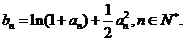
(1)求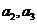 ,
,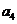 并求数列
并求数列 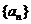 的通项公式;
的通项公式;
(2)对一切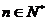 ,证明
,证明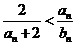 成立;
成立;
(3)记数列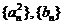 的前
的前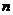 项和分别是
项和分别是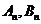 ,证明
,证明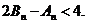
20.解:(1)因为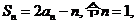
解得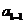 …………1分
…………1分
再分别令n=2,n=3,解得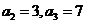 …………3分
…………3分
(2)因为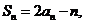
所以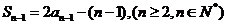
两式相减得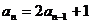
所以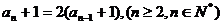
又因为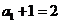 ,所以
,所以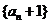 是首项为2,公比为2的等比数列
是首项为2,公比为2的等比数列
所以 ,所以
,所以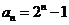 …………7分
…………7分
(3)因为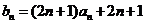 ,
,
所以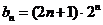
所以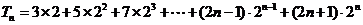 ①
①
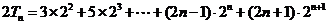 ②
②
①-②得: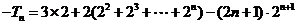
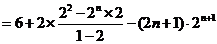

所以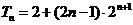 …………10分
…………10分
若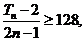
则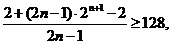
即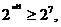 所以
所以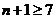 ,解得
,解得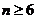 ,
,
所以满足不等式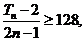 的最小n值6, …………12分
的最小n值6, …………12分
20.(天津市六校2010届高三第三次联考文科)(本小题满分12分)
已知数列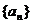 的前n项和为
的前n项和为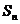 ,且满足
,且满足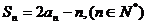
(1)求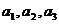 的值;
的值;
(2)求数列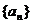 的通项公式;
的通项公式;
(3)若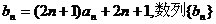 的前n项和为
的前n项和为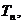 求满足不等式
求满足不等式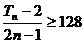 的最小n值.
的最小n值.
21.解:(I)∵点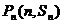 在函数
在函数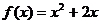 的图像上,
的图像上,
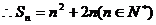 …………2分
…………2分
当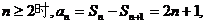
当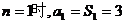 满足上式,
满足上式,
所以数列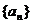 的通项公式为
的通项公式为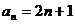 …………4分
…………4分
(II)由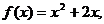 求导得
求导得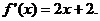
∵在点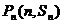 处的切线的斜率为
处的切线的斜率为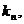
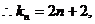 …………5分
…………5分
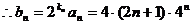
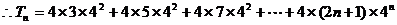
用错位相减法可求得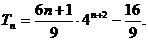 …………9分
…………9分
(III)
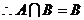
又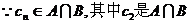 中的最小数,
中的最小数,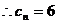
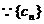 的公差是4的倍数,
的公差是4的倍数,
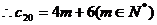 …………11分
…………11分
有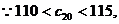
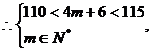 解得m=27.
解得m=27.
所以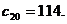
设等差数列的公差为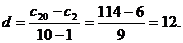
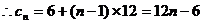 ,即为
,即为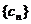 的通项公式 …………14分
的通项公式 …………14分
21.(天津市六校2010届高三第三次联考理科)(本小题14分)
已知数列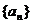 的前n项和为
的前n项和为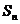 ,对一切正整数n,点
,对一切正整数n,点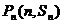 都在函数
都在函数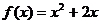 的图像上,且在点
的图像上,且在点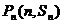 处的切线的斜率为
处的切线的斜率为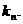
(I)求数列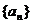 的通项公式;
的通项公式;
(II)若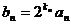 ,求数列
,求数列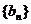 的前n项和
的前n项和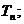
(III)设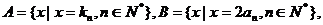 等差数列
等差数列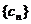 的任一项
的任一项 ,其中c1是
,其中c1是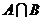 的最小数,
的最小数, 求数列
求数列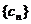 的通项公式.
的通项公式.
22.(天津市武清区2009-2010学年高三下学期第一次模拟文)(本小题满分14分)
已知正项数列{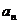 }满足
}满足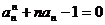 (
(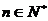 )
)
(1)求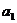 ,
,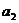 ;
;
(2)求证: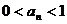
(3)求证: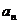 >
>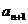 ;
;
(1)∵ 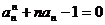 ,
,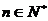
令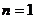 得
得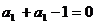 ∴
∴ 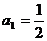 ………………1分
………………1分
令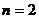 得
得 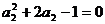 ∴
∴ 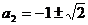
∵ 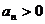 ∴
∴ 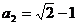 ……………………………3分
……………………………3分
(2)∵ 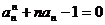 ∴
∴ 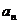 是方程
是方程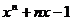 的一个根 ………4分
的一个根 ………4分
设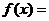
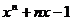 ,则
,则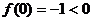 ,
,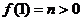 。
。
∴ 方程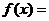 0在(0,1)内至少有一个根。
…………………6分
0在(0,1)内至少有一个根。
…………………6分
∵ 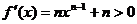 ∴
∴ 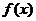 在(0,+∞)上是增函数,…………7分
在(0,+∞)上是增函数,…………7分
∴ 方程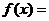 0在(0,+∞)上有唯一的根,且根在(0,1)内,
0在(0,+∞)上有唯一的根,且根在(0,1)内,
∴ 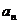 ∈(0,1) ∴
∈(0,1) ∴ 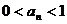 ………………………………9分
………………………………9分
(3)∵ 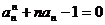 ,∴
,∴ 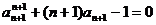
两式相减得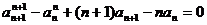 …………………10分
…………………10分
若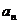 ≤
≤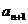 ,∵
,∵ 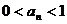 则
则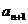 ≥
≥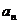 >
>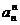 ,
,
从而有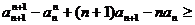
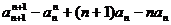
=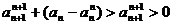 , ……………………………13分
, ……………………………13分
与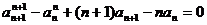 矛盾,
矛盾,
∴ 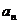 >
>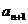 ……………………………………………14分
……………………………………………14分
22.(天津市武清区2009-2010学年高三下学期第一次模拟理)(本小题满分14分)
已知正项数列{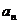 }满足
}满足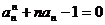 (
(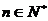 )
)
(1)求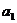 ,
,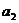 ;
;
(2)求证: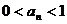
(3)求证: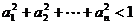 。
。
解: (1)∵ 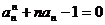 ,
,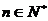
令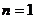 得
得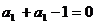 ∴
∴ 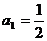 ………………1分
………………1分
令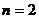 得
得 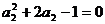 ∴
∴ 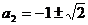
∵ 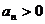 ∴
∴ 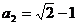 ……………………………3分
……………………………3分
(2)∵ 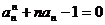 ∴
∴ 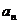 是方程
是方程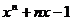 的一个根 ………4分
的一个根 ………4分
设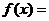
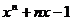 ,则
,则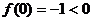 ,
,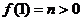 。
。
∴ 方程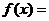 0在(0,1)内至少有一个根。
…………………6分
0在(0,1)内至少有一个根。
…………………6分
∵ 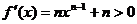 ∴
∴ 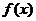 在(0,+∞)上是增函数,…………7分
在(0,+∞)上是增函数,…………7分
∴ 方程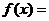 0在(0,+∞)上有唯一的根,且根在(0,1)内,
0在(0,+∞)上有唯一的根,且根在(0,1)内,
∴ 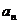 ∈(0,1) ∴
∈(0,1) ∴ 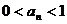 ………………………………9分
………………………………9分
(3)当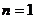 时,
时,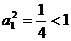 原式成立。………………………10分
原式成立。………………………10分
当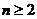 时,∵
时,∵ 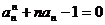 且
且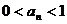
∴ 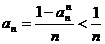 ……………………11分
……………………11分
∴ 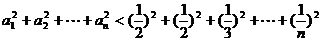
<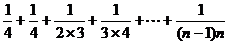
=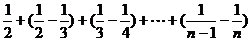
=1-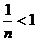 ………………………………………13分
………………………………………13分
综上,∴ 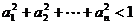 …………………………14分
…………………………14分
21. (天津市河西区2010届高三第一次模拟理科)(14分)
已知数列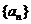 中,
中,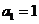 ,且点
,且点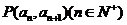 在直线
在直线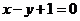 上。
上。
求数列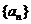 的通项公式;[来源:高&考%资(源#网
的通项公式;[来源:高&考%资(源#网
若函数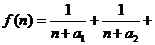 ……+
……+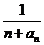
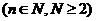 ,求函数
,求函数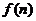 的最小值;
的最小值;
设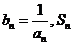 表示数列
表示数列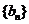 的前
的前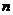 项和。试问:是否存在关于
项和。试问:是否存在关于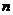 的模式
的模式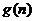 ,使得
,使得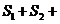 ……+
……+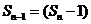 ·
·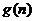 对于一切不小于2的自然数恒成立?若存在,写出
对于一切不小于2的自然数恒成立?若存在,写出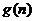 的解析式,并加以证明;若不存在,请说明理由。
的解析式,并加以证明;若不存在,请说明理由。

22.解:(Ⅰ)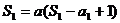 ∴
∴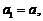 ………………1分
………………1分
当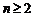 时,
时, 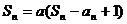
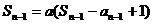
两式相减得: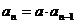 ,
,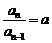
即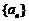 是等比数列.∴
是等比数列.∴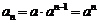 ;
……………………4分
;
……………………4分
(Ⅱ)由(Ⅰ)知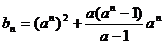 ,
,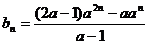 ,
,
若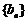 为等比数列,则有
为等比数列,则有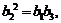 ……………………5分
……………………5分
而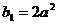 ,
,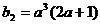 ,
,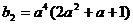 ……………………6分
……………………6分
故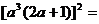
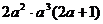 ,解得
,解得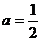 ,……………………………7分
,……………………………7分
再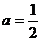 将代入得
将代入得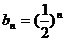 成立,
成立,
所以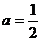 .
………………………………………………………………8分
.
………………………………………………………………8分
(III)证明:由(Ⅱ)知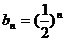 ,
,
所以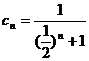
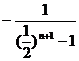 ,………………… 9分
,………………… 9分
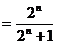
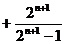
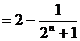
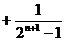 ……………… 11分
……………… 11分
所以
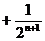 …………………… 12分
…………………… 12分
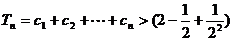

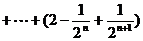

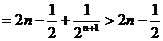 …………………………14分
…………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com