
题目列表(包括答案和解析)
2.对于函数 ,下列命题中正确的是: A.
,下列命题中正确的是: A. B.
B.
C. D.
D.
1.设集合 ,则正确的是: A.
,则正确的是: A. B.
B.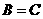 C.
C. D.
D.
2、特例法:就是运用满足题设条件的某些特殊数值、特殊位置、特殊关系、特殊图形、特殊数列、特殊函数等对各选择支进行检验或推理,利用问题在某一特殊情况下不真,则它在一般情况下也不真的原理,由此判明选项真伪的方法。用特例法解选择题时,特例取得愈简单、愈特殊愈好。
(1)特殊值
例5、若sinα>tanα>cotα( ),则α∈( )
),则α∈( )
A.( ,
, ) B.(
) B.( ,0) C.(0,
,0) C.(0, ) D.(
) D.( ,
, )
)
解析:因 ,取α=-
,取α=- 代入sinα>tanα>cotα,满足条件式,则排除A、C、D,故选B。
代入sinα>tanα>cotα,满足条件式,则排除A、C、D,故选B。
例6、一个等差数列的前n项和为48,前2n项和为60,则它的前3n项和为( )
A.-24 B.84 C.72 D.36
解析:结论中不含n,故本题结论的正确性与n取值无关,可对n取特殊值,如n=1,此时a1=48,a2=S2-S1=12,a3=a1+2d= -24,所以前3n项和为36,故选D。
(2)特殊函数
例7、如果奇函数f(x) 是[3,7]上是增函数且最小值为5,那么f(x)在区间[-7,-3]上是( )
A.增函数且最小值为-5 B.减函数且最小值是-5
C.增函数且最大值为-5 D.减函数且最大值是-5
解析:构造特殊函数f(x)= x,虽然满足题设条件,并易知f(x)在区间[-7,-3]上是增函数,且最大值为f(-3)=-5,故选C。
x,虽然满足题设条件,并易知f(x)在区间[-7,-3]上是增函数,且最大值为f(-3)=-5,故选C。
例8、定义在R上的奇函数f(x)为减函数,设a+b≤0,给出下列不等式:①f(a)·f(-a)≤0;②f(b)·f(-b)≥0;③f(a)+f(b)≤f(-a)+f(-b);④f(a)+f(b)≥f(-a)+f(-b)。其中正确的不等式序号是( )
A.①②④ B.①④ C.②④ D.①③
解析:取f(x)= -x,逐项检查可知①④正确。故选B。
(3)特殊数列
例9、已知等差数列 满足
满足 ,则有 ( )
,则有 ( )
A、 B、
B、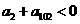 C、
C、 D、
D、
解析:取满足题意的特殊数列 ,则
,则 ,故选C。
,故选C。
(4)特殊位置
例10、过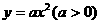 的焦点
的焦点 作直线交抛物线与
作直线交抛物线与 两点,若
两点,若 与
与 的长分别是
的长分别是 ,则
,则 ( )
( )
A、 B、
B、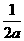 C、
C、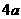 D、
D、

解析:考虑特殊位置PQ⊥OP时, ,所以
,所以 ,故选C。
,故选C。
例11、向高为 的水瓶中注水,注满为止,如果注水量
的水瓶中注水,注满为止,如果注水量 与水深
与水深 的函数关系的图象如图所示,那么水瓶的形状是 ( )
的函数关系的图象如图所示,那么水瓶的形状是 ( )


解析:取 ,由图象可知,此时注水量
,由图象可知,此时注水量 大于容器容积的
大于容器容积的 ,故选B。
,故选B。
(5)特殊点
例12、设函数 ,则其反函数
,则其反函数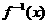 的图像是 ( )
的图像是 ( )
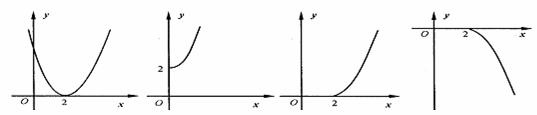
A、 B、 C、 D、
解析:由函数 ,可令x=0,得y=2;令x=4,得y=4,则特殊点(2,0)及(4,4)都应在反函数f-1(x)的图像上,观察得A、C。又因反函数f-1(x)的定义域为
,可令x=0,得y=2;令x=4,得y=4,则特殊点(2,0)及(4,4)都应在反函数f-1(x)的图像上,观察得A、C。又因反函数f-1(x)的定义域为 ,故选C。
,故选C。
(6)特殊方程
例13、双曲线b2x2-a2y2=a2b2 (a>b>0)的渐近线夹角为α,离心率为e,则cos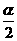 等于( )
等于( )
A.e B.e2 C.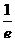 D.
D.
解析:本题是考查双曲线渐近线夹角与离心率的一个关系式,故可用特殊方程来考察。取双曲线方程为 -
-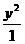 =1,易得离心率e=
=1,易得离心率e=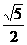 ,cos
,cos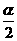 =
= ,故选C。
,故选C。
(7)特殊模型
例14、如果实数x,y满足等式(x-2)2+y2=3,那么 的最大值是( )
的最大值是( )
A. B.
B. C.
C.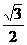 D.
D.
解析:题中 可写成
可写成 。联想数学模型:过两点的直线的斜率公式k=
。联想数学模型:过两点的直线的斜率公式k= ,可将问题看成圆(x-2)2+y2=3上的点与坐标原点O连线的斜率的最大值,即得D。
,可将问题看成圆(x-2)2+y2=3上的点与坐标原点O连线的斜率的最大值,即得D。
1、直接法:就是从题设条件出发,通过正确的运算、推理或判断,直接得出结论再与选择支对照,从而作出选择的一种方法。运用此种方法解题需要扎实的数学基础。
例1、某人射击一次击中目标的概率为0.6,经过3次射击,此人至少有2次击中目标的概率为 ( )

解析:某人每次射中的概率为0.6,3次射击至少射中两次属独立重复实验。
 故选A。
故选A。
例2、有三个命题:①垂直于同一个平面的两条直线平行;②过平面α的一条斜线l有且仅有一个平面与α垂直;③异面直线a、b不垂直,那么过a的任一个平面与b都不垂直。其中正确命题的个数为( )
A.0 B.1 C.2 D.3
解析:利用立几中有关垂直的判定与性质定理对上述三个命题作出判断,易得都是正确的,故选D。
例3、已知F1、F2是椭圆 +
+ =1的两焦点,经点F2的的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( )
=1的两焦点,经点F2的的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( )
A.11 B.10 C.9 D.16
解析:由椭圆的定义可得|AF1|+|AF2|=2a=8,|BF1|+|BF2|=2a=8,两式相加后将|AB|=5=|AF2|+|BF2|代入,得|AF1|+|BF1|=11,故选A。
例4、已知 在[0,1]上是
在[0,1]上是 的减函数,则a的取值范围是( )
的减函数,则a的取值范围是( )
A.(0,1) B.(1,2) C.(0,2) D.[2,+∞)
解析:∵a>0,∴y1=2-ax是减函数,∵  在[0,1]上是减函数。
在[0,1]上是减函数。
∴a>1,且2-a>0,∴1<a<2,故选B。
2、对于选择题一定要小题小做,小题巧做,切忌小题大做。“不择手段,多快好省”是解选择题的基本宗旨。
7、估算法:就是把复杂问题转化为较简单的问题,求出答案的近似值,或把有关数值扩大或缩小,从而对运算结果确定出一个范围或作出一个估计,进而作出判断的方法。
例28、农民收入由工资性收入和其它收入两部分构成。03年某地区农民人均收入为3150元(其中工资源共享性收入为1800元,其它收入为1350元),预计该地区自04年起的5年内,农民的工资源共享性收入将以每年的年增长率增长,其它性收入每年增加160元。根据以上数据,08年该地区人均收入介于 ( )
(A)4200元~4400元 (B)4400元~4460元
(C)4460元~4800元 (D)4800元~5000元
解析:08年农民工次性人均收入为:




又08年农民其它人均收入为1350+160 =2150
=2150
故08年农民人均总收入约为2405+2150=4555(元)。故选B。
说明:1、解选择题的方法很多,上面仅列举了几种常用的方法,这里由于限于篇幅,其它方法不再一一举例。需要指出的是对于有些题在解的过程中可以把上面的多种方法结合起来进行解题,会使题目求解过程简单化。
6、分析法:就是对有关概念进行全面、正确、深刻的理解或对有关信息提取、分析和加工后而作出判断和选择的方法。
(1)特征分析法--根据题目所提供的信息,如数值特征、结构特征、位置特征等,进行快速推理,迅速作出判断的方法,称为特征分析法。
例23、如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联,连线标的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传送信息,信息可以分开沿不同的路线同时传送,则单位时间内传递的最大信息量为( )

A.26 B.24 C.20 D.19
解析:题设中数字所标最大通信量是限制条件,每一支要以最小值来计算,否则无法同时传送,则总数为3+4+6+6=19,故选D。
例24、设球的半径为R, P、Q是球面上北纬600圈上的两点,这两点在纬度圈上的劣弧的长是 ,则这两点的球面距离是
,则这两点的球面距离是
A、 B、
B、 C、
C、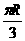 D、
D、
解析:因纬线弧长>球面距离>直线距离,排除A、B、D,故选C。
例25、已知 ,则
,则 等于 ( )
等于 ( )
A、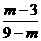 B、
B、 C、
C、 D、
D、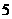
解析:由于受条件sin2θ+cos2θ=1的制约,故m为一确定的值,于是sinθ,cosθ的值应与m的值无关,进而推知tan 的值与m无关,又
的值与m无关,又 <θ<π,
<θ<π, <
< <
< ,∴tan
,∴tan >1,故选D。
>1,故选D。
(2)逻辑分析法--通过对四个选择支之间的逻辑关系的分析,达到否定谬误支,选出正确支的方法,称为逻辑分析法。
例26、设a,b是满足ab<0的实数,那么
A.|a+b|>|a-b| B.|a+b|<|a-b|
C.|a-b|<|a|-|b| D.|a-b|<|a|+|b|
解析:∵A,B是一对矛盾命题,故必有一真,从而排除错误支C,D。又由ab<0,可令a=1,b= -1,代入知B为真,故选B。
例27、 的三边
的三边 满足等式
满足等式 ,则此三角形必是()
,则此三角形必是()
A、以 为斜边的直角三角形 B、以
为斜边的直角三角形 B、以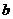 为斜边的直角三角形
为斜边的直角三角形
C、等边三角形 D、其它三角形
解析:在题设条件中的等式是关于 与
与 的对称式,因此选项在A、B为等价命题都被淘汰,若选项C正确,则有
的对称式,因此选项在A、B为等价命题都被淘汰,若选项C正确,则有 ,即
,即 ,从而C被淘汰,故选D。
,从而C被淘汰,故选D。
5、筛选法(也叫排除法、淘汰法):就是充分运用选择题中单选题的特征,即有且只有一个正确选择支这一信息,从选择支入手,根据题设条件与各选择支的关系,通过分析、推理、计算、判断,对选择支进行筛选,将其中与题设相矛盾的干扰支逐一排除,从而获得正确结论的方法。使用筛选法的前提是“答案唯一”,即四个选项中有且只有一个答案正确。
例20、若x为三角形中的最小内角,则函数y=sinx+cosx的值域是( )
A.(1,
 B.(0,
B.(0,
 C.[
C.[ ,
, ] D.(
] D.( ,
,

解析:因 为三角形中的最小内角,故
为三角形中的最小内角,故 ,由此可得y=sinx+cosx>1,排除B,C,D,故应选A。
,由此可得y=sinx+cosx>1,排除B,C,D,故应选A。
例21、原市话资费为每3分钟0.18元,现调整为前3分钟资费为0.22元,超过3分钟的,每分钟按0.11元计算,与调整前相比,一次通话提价的百分率( )
A.不会提高70% B.会高于70%,但不会高于90%
C.不会低于10% D.高于30%,但低于100%
解析:取x=4,y=·100%≈-8.3%,排除C、D;取x=30,y = ·100%≈77.2%,排除A,故选B。
例22、给定四条曲线:① ,②
,② ,③
,③ ,④
,④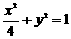 ,其中与直线
,其中与直线 仅有一个交点的曲线是( )
仅有一个交点的曲线是( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
解析:分析选择支可知,四条曲线中有且只有一条曲线不符合要求,故可考虑找不符合条件的曲线从而筛选,而在四条曲线中②是一个面积最大的椭圆,故可先看②,显然直线和曲线 是相交的,因为直线上的点
是相交的,因为直线上的点 在椭圆内,对照选项故选D。
在椭圆内,对照选项故选D。
4、验证法:就是将选择支中给出的答案或其特殊值,代入题干逐一去验证是否满足题设条件,然后选择符合题设条件的选择支的一种方法。在运用验证法解题时,若能据题意确定代入顺序,则能较大提高解题速度。
例18、计算机常用的十六进制是逢16进1的计数制,采用数字0-9和字母A-F共16个计数符号,这些符号与十进制的数的对应关系如下表:
|
十六进制 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
十进制 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
例如:用十六进制表示E+D=1B,则A×B= ( )
A.6E B.72 C.5F D.BO
解析:采用代入检验法,A×B用十进制数表示为1×11=110,而
6E用十进制数表示为6×16+14=110;72用十进制数表示为7×16+2=114
5F用十进制数表示为5×16+15=105;B0用十进制数表示为11×16+0=176,故选A。
例19、方程 的解
的解 ( )
( )
A.(0,1) B.(1,2) C.(2,3) D.(3,+∞)
解析:若 ,则
,则 ,则
,则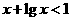 ;若
;若 ,则
,则 ,则
,则 ;若
;若 ,则
,则 ,则
,则 ;若
;若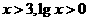 ,则
,则 ,故选C。
,故选C。
3、图解法:就是利用函数图像或数学结果的几何意义,将数的问题(如解方程、解不等式、求最值,求取值范围等)与某些图形结合起来,利用直观几性,再辅以简单计算,确定正确答案的方法。这种解法贯穿数形结合思想,每年高考均有很多选择题(也有填空题、解答题)都可以用数形结合思想解决,既简捷又迅速。
例15、已知α、β都是第二象限角,且cosα>cosβ,则( )

A.α<β B.sinα>sinβ
C.tanα>tanβ D.cotα<cotβ
解析:在第二象限角内通过余弦函数线cosα>cosβ找出α、β的终边位置关系,再作出判断,得B。
例16、已知 、
、 均为单位向量,它们的夹角为60°,那么|
均为单位向量,它们的夹角为60°,那么| +3
+3 |=
|=
A. B.
B. C.
C. D.4
D.4
解析:如图, +3
+3 =
=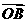 ,在
,在 中,
中, 由余弦定理得|
由余弦定理得| +3
+3 |=|
|=|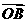 |=
|= ,故选C。
,故选C。
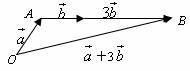
例17、已知{an}是等差数列,a1=-9,S3=S7,那么使其前n项和Sn最小的n是( )
A.4 B.5 C.6 D.7
解析:等差数列的前n项和Sn= n2+(a1-
n2+(a1- )n可表示为过原点的抛物线,又本题中a1=-9<0,
S3=S7,可表示如图,由图可知,n=
)n可表示为过原点的抛物线,又本题中a1=-9<0,
S3=S7,可表示如图,由图可知,n=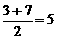 ,是抛物线的对称轴,所以n=5是抛物线的对称轴,所以n=5时Sn最小,故选B。
,是抛物线的对称轴,所以n=5是抛物线的对称轴,所以n=5时Sn最小,故选B。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com