
题目列表(包括答案和解析)
11.平移公式:(1)按向量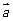 把
把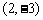 平移到
平移到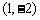 ,则按向量
,则按向量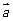 把点
把点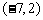 平移到点______(答:(-8,3));(2)函数
平移到点______(答:(-8,3));(2)函数 的图象按向量
的图象按向量 平移后,所得函数的解析式是
平移后,所得函数的解析式是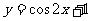 ,则
,则 =________(答:
=________(答: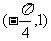 )
)
10.线段的定比分点:
若点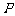 分
分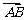 所成的比为
所成的比为 ,则
,则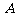 分
分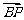 所成的比为_______(答:
所成的比为_______(答: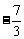 )
)
(1)若M(-3,-2),N(6,-1),且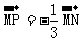 ,则点P的坐标为_______(答:
,则点P的坐标为_______(答: );(2)已知
);(2)已知 ,直线
,直线 与线段
与线段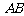 交于
交于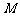 ,且
,且 ,则
,则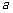 等于_______(答:2或-4)
等于_______(答:2或-4)
7、向量的运算律:下列命题中:① 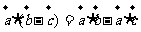 ;②
;②  ;③
;③ 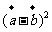

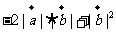 ;④ 若
;④ 若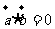 ,则
,则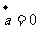 或
或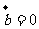 ;⑤若
;⑤若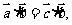 则
则 ;⑥
;⑥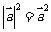 ;⑦
;⑦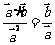 ;⑧
;⑧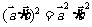 ;⑨
;⑨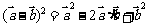 。其中正确的是______(答:①⑥⑨)
。其中正确的是______(答:①⑥⑨)
(1)若向量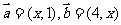 ,当
,当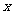 =_____时
=_____时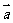 与
与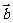 共线且方向相同(答:2);(2)已知
共线且方向相同(答:2);(2)已知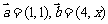 ,
, ,
, ,且
,且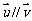 ,则x=______(答:4);(3)设
,则x=______(答:4);(3)设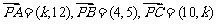 ,则k=_____时,A,B,C共线(答:-2或11)
,则k=_____时,A,B,C共线(答:-2或11)
(1)已知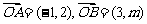 ,若
,若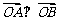 ,则
,则 (答:
(答: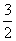 );(2)以原点O和A(4,2)为两个顶点作等腰直角三角形OAB,
);(2)以原点O和A(4,2)为两个顶点作等腰直角三角形OAB,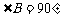 ,则点B的坐标是________
(答:(1,3)或(3,-1));(3)已知
,则点B的坐标是________
(答:(1,3)或(3,-1));(3)已知 向量
向量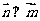 ,且
,且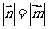 ,则
,则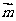 的坐标是________ (答:
的坐标是________ (答: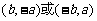 )
)
6、向量的运算:
(1)几何运算:
(1)化简:①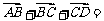 ___;②
___;②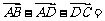 ____;③
____;③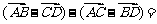 _____(答:①
_____(答:①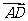 ;②
;②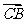 ;③
;③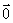 );(2)若正方形
);(2)若正方形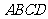 的边长为1,
的边长为1, ,则
,则 =_____(答:
=_____(答: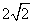 );(3)若O是
);(3)若O是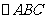 所在平面内一点,且满足
所在平面内一点,且满足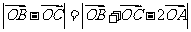 ,则
,则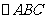 的形状为____(答:直角三角形);(4)若
的形状为____(答:直角三角形);(4)若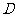 为
为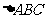 的边
的边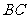 的中点,
的中点,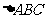 所在平面内有一点
所在平面内有一点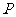 ,满足
,满足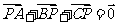 ,设
,设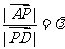 ,则
,则 的值为___(答:2);(5)若点
的值为___(答:2);(5)若点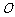 是
是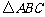 的外心,且
的外心,且 ,则
,则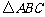 的内角
的内角 为____(答:
为____(答: );
);
(2)坐标运算:(1)已知点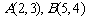 ,
,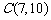 ,若
,若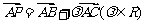 ,则当
,则当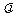 =____时,点P在第一、三象限的角平分线上(答:
=____时,点P在第一、三象限的角平分线上(答: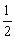 );(2)已知
);(2)已知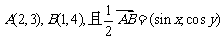 ,
,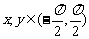 ,则
,则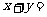 (答:
(答: 或
或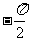 );(3)已知作用在点
);(3)已知作用在点 的三个力
的三个力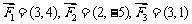 ,则合力
,则合力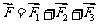 的终点坐标是 (答:(9,1))
的终点坐标是 (答:(9,1))
设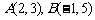 ,且
,且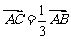 ,
,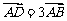 ,则C、D的坐标分别是__________(答:
,则C、D的坐标分别是__________(答: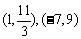 );
);
已知向量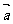 =(sinx,cosx),
=(sinx,cosx),  =(sinx,sinx),
=(sinx,sinx), 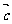 =(-1,0)。(1)若x=
=(-1,0)。(1)若x=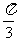 ,求向量
,求向量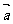 、
、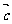 的夹角;(2)若x∈
的夹角;(2)若x∈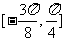 ,函数
,函数 的最大值为
的最大值为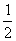 ,求
,求 的值(答:
的值(答: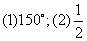 或
或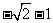 );
);
已知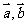 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为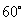 ,那么
,那么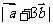 =_____(答:
=_____(答: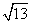 );
);
如图,在平面斜坐标系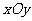 中,
中, ,平面上任一点P关于斜坐标系的斜坐标是这样定义的:若
,平面上任一点P关于斜坐标系的斜坐标是这样定义的:若 ,其中
,其中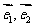 分别为与x轴、y轴同方向的单位向量,则P点斜坐标为
分别为与x轴、y轴同方向的单位向量,则P点斜坐标为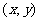 。(1)若点P的斜坐标为(2,-2),求P到O的距离|PO|;(2)求以O为圆心,1为半径的圆在斜坐标系
。(1)若点P的斜坐标为(2,-2),求P到O的距离|PO|;(2)求以O为圆心,1为半径的圆在斜坐标系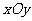 中的方程。(答:(1)2;(2)
中的方程。(答:(1)2;(2) );
);
5、平面向量的数量积:
(1)△ABC中,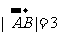 ,
,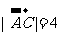 ,
,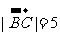 ,则
,则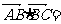 _________(答:-9);(2)已知
_________(答:-9);(2)已知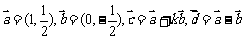 ,
,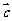 与
与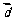 的夹角为
的夹角为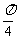 ,则
,则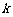 等于____(答:1);(3)已知
等于____(答:1);(3)已知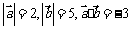 ,则
,则 等于____(答:
等于____(答: );(4)已知
);(4)已知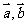 是两个非零向量,且
是两个非零向量,且 ,则
,则 的夹角为____(答:
的夹角为____(答: )
)
已知 ,
,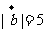 ,且
,且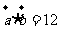 ,则向量
,则向量 在向量
在向量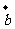 上的投影为______(答:
上的投影为______(答: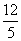 )
)
(1)已知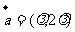 ,
, ,如果
,如果 与
与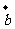 的夹角为锐角,则
的夹角为锐角,则 的取值范围是______(答:
的取值范围是______(答: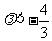 或
或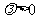 且
且 );(2)已知
);(2)已知 的面积为
的面积为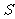 ,且
,且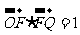 ,若
,若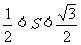 ,则
,则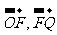 夹角
夹角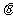 的取值范围是_________(答:
的取值范围是_________(答: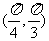 );(3)已知
);(3)已知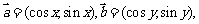
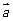 与
与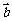 之间有关系式
之间有关系式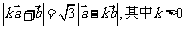 ,①用
,①用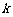 表示
表示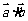 ;②求
;②求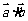 的最小值,并求此时
的最小值,并求此时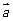 与
与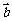 的夹角
的夹角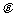 的大小(答:①
的大小(答:①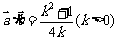 ;②最小值为
;②最小值为 ,
,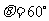 )
)
4、实数与向量的积
2、向量的表示方法:(1)若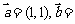
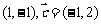 ,则
,则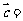 ______(答:
______(答: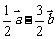 );(2)下列向量组中,能作为平面内所有向量基底的是 A.
);(2)下列向量组中,能作为平面内所有向量基底的是 A. 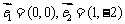 B.
B. 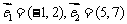 C.
C. 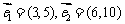 D.
D. 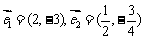 (答:B);(3)已知
(答:B);(3)已知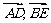 分别是
分别是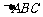 的边
的边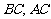 上的中线,且
上的中线,且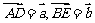 ,则
,则 可用向量
可用向量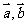 表示为_____(答:
表示为_____(答: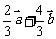 );(4)已知
);(4)已知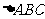 中,点
中,点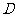 在
在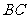 边上,且
边上,且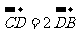 ,
,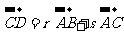 ,则
,则 的值是___(答:0)
的值是___(答:0)
1、向量有关概念:
(1)向量的概念:已知A(1,2),B(4,2),则把向量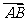 按向量
按向量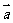 =(-1,3)平移后得到的向量是_____(答:(3,0))
=(-1,3)平移后得到的向量是_____(答:(3,0))
下列命题:(1)若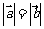 ,则
,则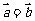 。(2)两个向量相等的充要条件是它们的起点相同,终点相同。(3)若
。(2)两个向量相等的充要条件是它们的起点相同,终点相同。(3)若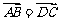 ,则
,则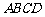 是平行四边形。(4)若
是平行四边形。(4)若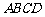 是平行四边形,则
是平行四边形,则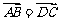 。(5)若
。(5)若 ,则
,则 。(6)若
。(6)若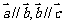 ,则
,则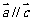 。其中正确的是_______(答:(4)(5))
。其中正确的是_______(答:(4)(5))
6.直线与圆锥曲线的位置关系:
(1)若直线y=kx+2与双曲线x2-y2=6的右支有两个不同的交点,则k的取值范围是_______(答:(-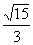 ,-1));(2)直线y―kx―1=0与椭圆
,-1));(2)直线y―kx―1=0与椭圆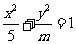 恒有公共点,则m的取值范围是_______(答:[1,5)∪(5,+∞));(3)过双曲线
恒有公共点,则m的取值范围是_______(答:[1,5)∪(5,+∞));(3)过双曲线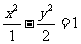 的右焦点直线交双曲线于A、B两点,若│AB︱=4,则这样的直线有_____条(答:3);
的右焦点直线交双曲线于A、B两点,若│AB︱=4,则这样的直线有_____条(答:3);
(2)过双曲线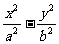 =1外一点
=1外一点 的直线与双曲线只有一个公共点的情况如下:①P点在两条渐近线之间且不含双曲线的区域内时,有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线,共四条;②P点在两条渐近线之间且包含双曲线的区域内时,有两条与渐近线平行的直线和只与双曲线一支相切的两条切线,共四条;③P在两条渐近线上但非原点,只有两条:一条是与另一渐近线平行的直线,一条是切线;④P为原点时不存在这样的直线;
的直线与双曲线只有一个公共点的情况如下:①P点在两条渐近线之间且不含双曲线的区域内时,有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线,共四条;②P点在两条渐近线之间且包含双曲线的区域内时,有两条与渐近线平行的直线和只与双曲线一支相切的两条切线,共四条;③P在两条渐近线上但非原点,只有两条:一条是与另一渐近线平行的直线,一条是切线;④P为原点时不存在这样的直线;
(3)过抛物线外一点总有三条直线和抛物线有且只有一个公共点:两条切线和一条平行于对称轴的直线。(1)过点 作直线与抛物线
作直线与抛物线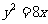 只有一个公共点,这样的直线有______(答:2);(2)过点(0,2)与双曲线
只有一个公共点,这样的直线有______(答:2);(2)过点(0,2)与双曲线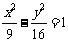 有且仅有一个公共点的直线的斜率的取值范围为______(答:
有且仅有一个公共点的直线的斜率的取值范围为______(答: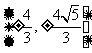 );(3)过双曲线
);(3)过双曲线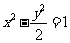 的右焦点作直线
的右焦点作直线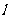 交双曲线于A、B两点,若
交双曲线于A、B两点,若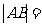 4,则满足条件的直线
4,则满足条件的直线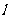 有____条(答:3);(4)对于抛物线C:
有____条(答:3);(4)对于抛物线C: ,我们称满足
,我们称满足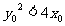 的点
的点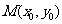 在抛物线的内部,若点
在抛物线的内部,若点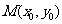 在抛物线的内部,则直线
在抛物线的内部,则直线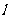 :
: 与抛物线C的位置关系是_______(答:相离);(5)过抛物线
与抛物线C的位置关系是_______(答:相离);(5)过抛物线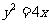 的焦点
的焦点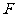 作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是
作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是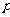 、
、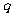 ,则
,则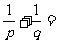 _______(答:1);(6)设双曲线
_______(答:1);(6)设双曲线 的右焦点为
的右焦点为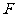 ,右准线为
,右准线为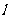 ,设某直线
,设某直线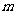 交其左支、右支和右准线分别于
交其左支、右支和右准线分别于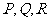 ,则
,则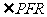 和
和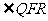 的大小关系为___________(填大于、小于或等于) (答:等于);(7)求椭圆
的大小关系为___________(填大于、小于或等于) (答:等于);(7)求椭圆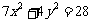 上的点到直线
上的点到直线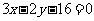 的最短距离(答:
的最短距离(答: );(8)直线
);(8)直线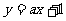 与双曲线
与双曲线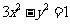 交于
交于 、
、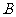 两点。①当
两点。①当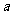 为何值时,
为何值时, 、
、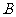 分别在双曲线的两支上?②当
分别在双曲线的两支上?②当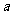 为何值时,以AB为直径的圆过坐标原点?(答:①
为何值时,以AB为直径的圆过坐标原点?(答:①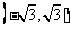 ;②
;②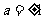 );
);
5、点 和椭圆
和椭圆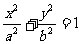 (
( )的关系:
)的关系:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com