
题目列表(包括答案和解析)
11.恒成立问题(1)设实数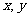 满足
满足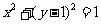 ,当
,当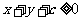 时,
时,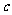 的取值范围是______(答:
的取值范围是______(答: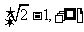 );(2)不等式
);(2)不等式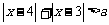 对一切实数
对一切实数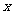 恒成立,求实数
恒成立,求实数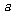 的取值范围_____(答:
的取值范围_____(答: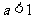 );(3)若不等式
);(3)若不等式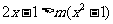 对满足
对满足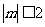 的所有
的所有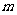 都成立,则
都成立,则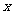 的取值范围_____(答:(
的取值范围_____(答:(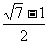 ,
,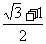 ));(4)若不等式
));(4)若不等式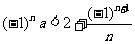 对于任意正整数
对于任意正整数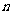 恒成立,则实数
恒成立,则实数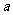 的取值范围是_____(答:
的取值范围是_____(答: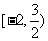 );(5)若不等式
);(5)若不等式 对
对 的所有实数
的所有实数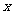 都成立,求
都成立,求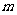 的取值范围.(答:
的取值范围.(答: )(6)已知不等式
)(6)已知不等式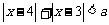 在实数集
在实数集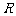 上的解集不是空集,求实数
上的解集不是空集,求实数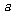 的取值范围______(答:
的取值范围______(答: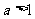 )
)
9、含参不等式的解法:(1)若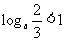 ,则
,则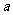 的取值范围是_____(答:
的取值范围是_____(答: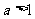 或
或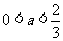 );(2)解不等式
);(2)解不等式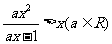 (答:
(答: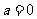 时,
时,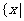
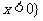 ;
;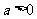 时,
时,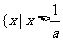 或
或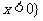 ;
;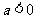 时,
时,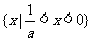 或
或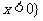 );(3)关于
);(3)关于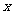 的不等式
的不等式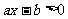 的解集为
的解集为 ,则不等式
,则不等式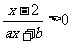 的解集为__________(答:(-1,2))
的解集为__________(答:(-1,2))
8.绝对值不等式的解法:解不等式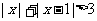 (答:
(答: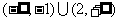 );若不等式
);若不等式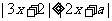 对
对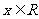 恒成立,则实数
恒成立,则实数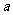 的取值范围为______。(答:
的取值范围为______。(答: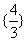 )
)
7.分式不等式的解法:(1)解不等式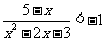 (答:
(答: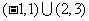 );
);
(2)关于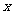 的不等式
的不等式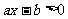 的解集为
的解集为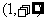 ,则关于
,则关于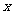 的不等式
的不等式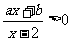 的解集为____________(答:
的解集为____________(答: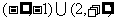 ).
).
6.简单的一元高次不等式的解法:(1)解不等式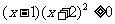 。(答:
。(答: 或
或 );(2)不等式
);(2)不等式 的解集是____(答:
的解集是____(答: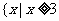 或
或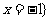 );(3)设函数
);(3)设函数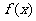 、
、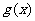 的定义域都是R,且
的定义域都是R,且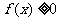 的解集为
的解集为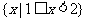 ,
,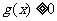 的解集为
的解集为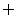 ,则不等式
,则不等式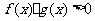 的解集为____(答:
的解集为____(答: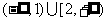 );(4)要使满足关于
);(4)要使满足关于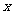 的不等式
的不等式 (解集非空)的每一个
(解集非空)的每一个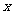 的值至少满足不等式
的值至少满足不等式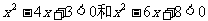 中的一个,则实数
中的一个,则实数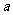 的取值范围是_____.(答:
的取值范围是_____.(答: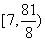 )
)
5、证明不等式的方法:
(1)已知 ,求证:
,求证: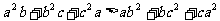 ;(2)
已知
;(2)
已知 ,求证:
,求证: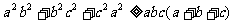 ;(3)已知
;(3)已知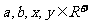 ,且
,且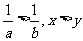 ,求证:
,求证: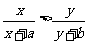 ;(4)已知
;(4)已知 ,求证:
,求证:
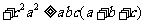 ;
;
4.常用不等式有:如果正数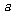 、
、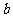 满足
满足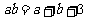 ,则
,则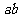 的取值范围是_____(答:
的取值范围是_____(答: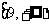 )
)
3. 利用重要不等式求函数最值
(1)下列命题中正确的是A、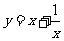 的最小值是2 B、
的最小值是2 B、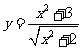 的最小值是2 C、
的最小值是2 C、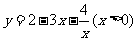 的最大值是
的最大值是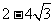 D、
D、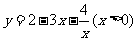 的最小值是
的最小值是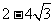 (答:C);(2)若
(答:C);(2)若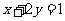 ,则
,则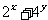 的最小值是______(答:
的最小值是______(答: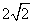 );(3)正数
);(3)正数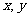 满足
满足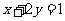 ,则
,则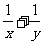 的最小值为______(答:
的最小值为______(答: );
);
(1)对于实数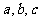 中,给出下列命题:①
中,给出下列命题:①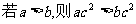 ;②
;② ;③
;③ ;④
;④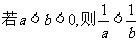 ;⑤
;⑤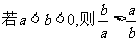 ; ⑥
; ⑥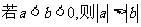 ;⑦
;⑦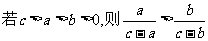 ;⑧
;⑧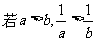 ,则
,则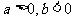 。其中正确的命题是______(答:②③⑥⑦⑧);
。其中正确的命题是______(答:②③⑥⑦⑧);
(2)已知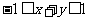 ,
,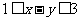 ,则
,则 的取值范围是______(答:
的取值范围是______(答: );
);
2. 不等式大小比较的常用方法:比较1+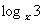 与
与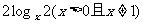 的大小(答:当
的大小(答:当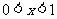 或
或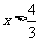 时,1+
时,1+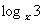 >
>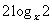 ;当
;当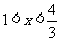 时,1+
时,1+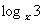 <
<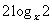 ;当
;当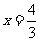 时,1+
时,1+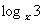 =
=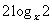 )
)
12、向量中一些常用的结论:
若⊿ABC的三边的中点分别为(2,1)、(-3,4)、 (-1,-1),则⊿ABC的重心的坐标为_______(答: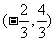 );
);
平面直角坐标系中,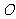 为坐标原点,已知两点
为坐标原点,已知两点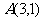 ,
,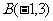 ,若点
,若点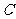 满足
满足
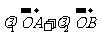 ,其中
,其中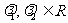 且
且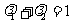 ,则点
,则点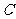 的轨迹是_______(答:直线AB)
的轨迹是_______(答:直线AB)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com