
题目列表(包括答案和解析)
6.主要思想与方法:
本章主要树立数形转化和结合的观点,以数代形,以形观数,用代数的运算处理几何问题,特别是处理向量的相关位置关系,正确运用共线向量和平面向量的基本定理,计算向量的模、两点的距离、向量的夹角,判断两向量是否垂直等。由于向量是一新的工具,它往往会与三角函数、数列、不等式、解几等结合起来进行综合考查,是知识的交汇点。
5. 向量的数量积:
(1)向量的夹角:
已知两个非零向量 与b,作
与b,作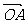 =
= ,
, 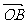 =b,则∠AOB=
=b,则∠AOB=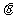 (
(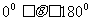 )叫做向量
)叫做向量 与b的夹角。
与b的夹角。
(2)两个向量的数量积:
已知两个非零向量 与b,它们的夹角为
与b,它们的夹角为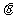 ,则
,则 ·b=︱
·b=︱ ︱·︱b︱cos
︱·︱b︱cos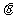 .
.
其中︱b︱cos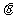 称为向量b在
称为向量b在 方向上的投影.
方向上的投影.
(3)向量的数量积的性质:
若 =(
=(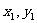 ),b=(
),b=(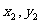 )则e·
)则e· =
= ·e=︱
·e=︱ ︱cos
︱cos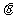 (e为单位向量);
(e为单位向量);
 ⊥b
⊥b
 ·b=0
·b=0
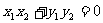 (
( ,b为非零向量);︱
,b为非零向量);︱ ︱=
︱=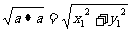 ;
;
cos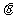 =
=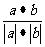 =
= .
.
(4)向量的数量积的运算律:
 ·b=b·
·b=b· ;(
;(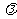
 )·b=
)·b=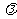 (
( ·b)=
·b)= ·(
·(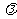 b);(
b);( +b)·c=
+b)·c= ·c+b·c.
·c+b·c.
4.P分有向线段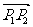 所成的比:
所成的比:
设P1、P2是直线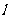 上两个点,点P是
上两个点,点P是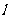 上不同于P1、P2的任意一点,则存在一个实数
上不同于P1、P2的任意一点,则存在一个实数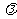 使
使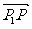 =
=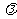
 ,
,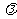 叫做点P分有向线段
叫做点P分有向线段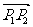 所成的比。
所成的比。
当点P在线段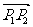 上时,
上时,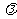 >0;当点P在线段
>0;当点P在线段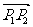 或
或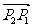 的延长线上时,
的延长线上时,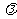 <0;
<0;
分点坐标公式:若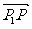 =
=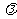
 ;
;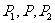 的坐标分别为(
的坐标分别为(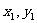 ),(
),(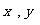 ),(
),(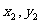 );则
);则 (
(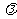 ≠-1), 中点坐标公式:
≠-1), 中点坐标公式:
 .
.
3.实数与向量的积:实数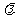 与向量
与向量 的积是一个向量。
的积是一个向量。
(1)︱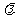
 ︱=︱
︱=︱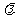 ︱·︱
︱·︱ ︱;
︱;
(2)
当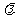 >0时,
>0时,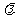
 与
与 的方向相同;当
的方向相同;当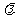 <0时,
<0时,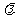
 与
与 的方向相反;当
的方向相反;当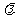 =0时,
=0时,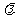
 =0.
=0.
(3)若 =(
=(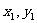 ),则
),则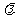 ·
· =(
=(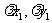 ).
).
两个向量共线的充要条件:
(1) 向量b与非零向量 共线的充要条件是有且仅有一个实数
共线的充要条件是有且仅有一个实数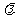 ,使得b=
,使得b=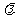
 .
.
(2) 若 =(
=(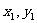 ),b=(
),b=(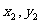 )则
)则 ∥b
∥b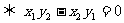 .
.
平面向量基本定理:
若e1、e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量 ,有且只有一对实数
,有且只有一对实数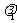 ,
,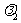 ,使得
,使得 =
=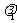 e1+
e1+ 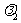 e2。
e2。
2. 加法与减法的代数运算:
(1)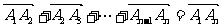 .
.
(2)若a=(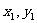 ),b=(
),b=(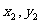 )则a
)则a b=(
b=( ).
).
向量加法与减法的几何表示:平行四边形法则、三角形法则。
以向量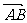 =
= 、
、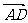 =
= 为邻边作平行四边形ABCD,则两条对角线的向量
为邻边作平行四边形ABCD,则两条对角线的向量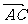 =
= +
+ ,
,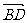 =
= -
- ,
,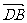 =
= -
-
且有︱ ︱-︱
︱-︱ ︱≤︱
︱≤︱

 ︱≤︱
︱≤︱ ︱+︱
︱+︱ ︱.
︱.
向量加法有如下规律: +
+ =
= +
+ (交换律);
(交换律);  +(
+( +c)=(
+c)=( +
+  )+c
(结合律);
)+c
(结合律);
 +0=
+0=
 +(-
+(- )=0.
)=0.
1.基本概念:
向量的定义、向量的模、零向量、单位向量、相反向量、共线向量、相等向量。
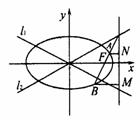
22、已知椭圆C的方程为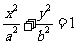 (a>b>0),双曲线
(a>b>0),双曲线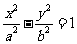 的两条渐近线为
的两条渐近线为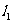 、
、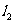 ,过椭圆C的右焦点F作直线l,使l⊥
,过椭圆C的右焦点F作直线l,使l⊥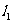 ,又l与
,又l与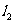 交于P点,设l与椭圆C的两交点从左到右依次为B、A(如图所示).求:
交于P点,设l与椭圆C的两交点从左到右依次为B、A(如图所示).求: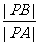 的最大值及取得最大值时椭圆C的率心率e的值.
的最大值及取得最大值时椭圆C的率心率e的值.
21、已知函数: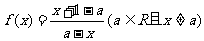 .
.
(1)证明:f(x)+2+f(2a-x)=0对定义域内的所有x都成立;
(2)当f(x)的定义域为[a+ ,a+1]时,求f(x)的值域。
,a+1]时,求f(x)的值域。
20、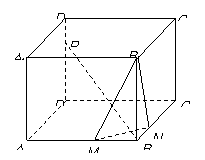 如图,M、N、P分别是正方体ABCD-A1B1C1D1的棱AB、BC、DD1上的点.
如图,M、N、P分别是正方体ABCD-A1B1C1D1的棱AB、BC、DD1上的点.
(1)若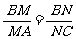 ,求证:无论点P在D1D上如何移动,总有BP⊥MN;
(2)若D1P : PD=1 : 2,且PB⊥平面B1MN,求二面角M-B1N-B的大小;
(3)棱DD1上是否存在点P,使得平面APC1⊥平面ACC1?证明你的结论.
,求证:无论点P在D1D上如何移动,总有BP⊥MN;
(2)若D1P : PD=1 : 2,且PB⊥平面B1MN,求二面角M-B1N-B的大小;
(3)棱DD1上是否存在点P,使得平面APC1⊥平面ACC1?证明你的结论.
19、已知函数f(x)=ax+b,当x∈[a1,b1]时,值域为[a2,b2],当x∈[a2,b2]时,值域是[a3,b3],…,当x∈[an-1,bn-1]时,值域为[an,bn],….其中a、b为常数,a1=0,b1=1.
(1)若a=1,求数列{an}与{bn}的通项公式;
(2)若a>0且a≠1,要使数列{bn}是公比不为1的等比数列,求b的值;
(3)若a>0,设数列{an}和{bn}的前n项和分别为Sn和Tn,求(T1+T2+…+T2000)- (S1+S2+…+S2000)的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com