
题目列表(包括答案和解析)
2.( )若等差数列的各项依次递减,且a2a4a6=45,a2+a4+a6=15,则数列{an}的通项公式为
A.2n-3 B.-2n+3 C.-2n+13 D.2n+9
1.( )已知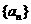 是等差数列,且公差
是等差数列,且公差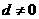 ,它们前
,它们前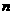 项和
项和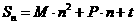 ,则
,则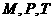 满足的关系是 A.
满足的关系是 A.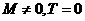 . B.
. B.
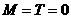 . C.
. C.
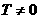 . D.
. D.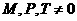
5.( B )在等差数列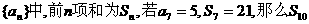 等于 ( )
等于 ( )
A.55 B.40 C.35 D.70
6设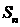 是等差数列
是等差数列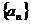 的前
的前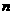 项和,已知
项和,已知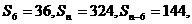 则
则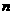 =______18____.
=______18____.
7在等差数列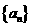 中,
中,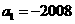 ,其前
,其前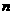 项的和为
项的和为 .若
.若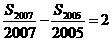 ,则
,则 _____-200_8_____
_____-200_8_____
例1已知数列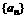 中,
中,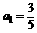 ,
,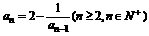 ,数列
,数列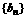 满足
满足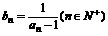
(1)
求证:数列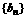 是等差数列;
是等差数列;
(2)
求数列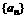 中的最大值和最小值,并说明理由
中的最大值和最小值,并说明理由
(1)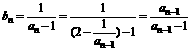 ,而
,而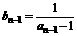 ,
,
∴ ,
,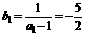 ;故数列
;故数列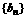 是首项为
是首项为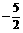 ,公差为1的等差数列;
,公差为1的等差数列;
(2)由(1)得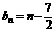 ,则
,则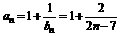 ;设函数
;设函数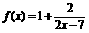 ,
,
函数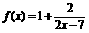 在
在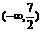 和
和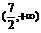 上均为减函数,当
上均为减函数,当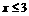 时,
时,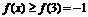 ;当
;当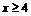 时,
时,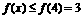 ;且
;且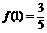 ,当
,当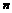 趋向于
趋向于 时,
时,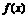 接近1,
接近1,
∴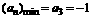 ,
,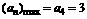 .
.
例2设等差数列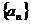 的前n项和为
的前n项和为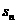 ,已知
,已知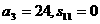 ,求:
,求:
①数列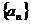 的通项公式 ②当n为何值时,
的通项公式 ②当n为何值时,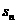 最大,最大值为多少?
最大,最大值为多少?
解析:由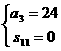 得
得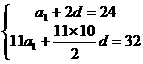 得
得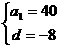
∴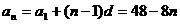

∴当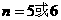 时,
时,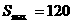
例3.在数列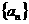 中,
中,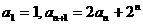 (1)设
(1)设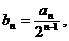 证明
证明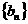 是等差数列;(2)求数列
是等差数列;(2)求数列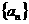 的前
的前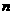 项和
项和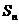 。
。
解析:(1)由已知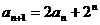 得
得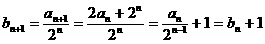 ,
,
又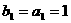

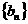 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;
(2)由(1)知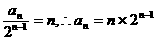
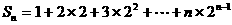
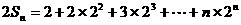
两式相减得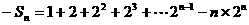
等差数列的性质同步练习题一 班级 姓名
21.已知数列{an}中,a1>0, 且an+1=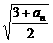 , (Ⅰ)试求a1的值,使得数列{an}是一个常数数列;
, (Ⅰ)试求a1的值,使得数列{an}是一个常数数列;
(Ⅱ)试求a1的取值范围,使得an+1>an对任何自然数n都成立;
(Ⅲ)若a1 = 2,设bn = | an+1-an| (n = 1,2,3,…),并以Sn表示数列{bn}的前n项的和,求证:Sn<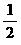 .
.
[思路分析]:解:(Ⅰ)欲使数列{an}是一个常数数列,则an+1=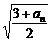 = an ……………………2’
= an ……………………2’
又依a1>0,可得an>0并解出:an=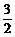 ,即a1 = an =
,即a1 = an =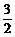 ……………………4’
……………………4’
(Ⅱ)研究an+1-an=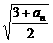 -
-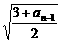 =
=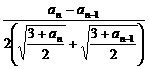 (n≥2) 注意到
(n≥2) 注意到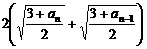 >0
>0
因此,可以得出:an+1-an,an-an-1,an-1-an-2,…,a2-a1有相同的符号……………7’
要使an+1>an对任意自然数都成立,只须a2-a1>0即可.由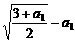 >0,解得:0<a1<
>0,解得:0<a1<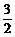 ………………9’
………………9’
(Ⅲ)用与(Ⅱ)中相同的方法,可得 当a1>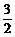 时,an+1<an对任何自然数n都成立.
时,an+1<an对任何自然数n都成立.
因此当a1=2时,an+1-an<0 ……………………………………………10’
∴ Sn= b1+b2+…bn=|a2-a1| + |a3-a2| +…+ |an+1-an|=a1-a2+a2-a3+…+an-an+1
=a1-an+1=2-an+1 ………………………………………………………13’
又:an+2=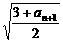 < an+1,可解得an+1>
< an+1,可解得an+1>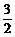 , 故Sn<2-
, 故Sn<2-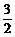 =
=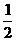 ………………………………………14’
………………………………………14’
20.已知函数f(x)=-x3+ax在(0,1)上是增函数.(1) 求实数a的取值集合A;
(2) 当a取A中最小值时,定义数列{an}满足:2an+1=f(an),且a1=b∈(0,1)(b为常数),试比较an+1与an的大小; (3) 在(2)的条件下,问是否存在正实数c.使0<<2对一切n∈N*恒成立?
(1)f'(x)=3x2+a>0,对x∈(0,1)恒成立,求出a≥3.………………4分
(2)当a=3时,由题意:an+1=-a+an,且a1=b∈(0,1)
以下用数学归纳法证明:an∈(0,1),对n∈N*恒成立.
①当n=1时,a1=b∈(0,1)成立;………………………………………………6分
②假设n=k时,ak∈(0,1)成立,那么当n=k+1时, ak+1=ak3+ak,由①知g(x)=(-x3+3x)
在(0,1)上单调递增,∴g(0)<g(ak)<g(1) 即0<ak+1<1, 由①②知对一切n∈N*都有an∈(0,1)
而an+1-an=-an3+an-an=an(1-an2)>0 ∴an+1>an…………………………………10分
(3)存在正实数c,使0<<2恒成立,令y==1+,在(c,+∞)上是减数,
∴随着an增大,而小, 又{an}为递增数列,所以要使0<<2恒成立,
只须∴0<c<,即0<c< ……… 14分
19.已知f(x+1)=x2-4,等差数列{an}中,a1=f(x-1), a2=-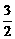 ,a3=f(x).(1)求x值;(2)求a2+a5+a8+…+a26的值.
,a3=f(x).(1)求x值;(2)求a2+a5+a8+…+a26的值.
[解] (1)∵f(x-1)=(x-1-1)2-4=(x-2)2-4 ∴f(x)=(x-1)2-4,∴a1=(x-2)2-4,a3=(x-1)2-4
又a1+a3=2a2,解得x=0或x=3.
(2)∵a1、a2、a3分别为0、-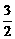 、-3或-3、-
、-3或-3、-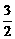 、0 ∴an=-
、0 ∴an=-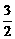 (n-1)或an=
(n-1)或an=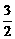 (n-3)
(n-3)
①当an=-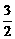 (n-1)时,a2+a5+…+a26=
(n-1)时,a2+a5+…+a26=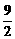 (a2+a26)=
(a2+a26)=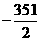
②当an=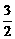 (n-3)时,a2+a5+…+a26=
(n-3)时,a2+a5+…+a26=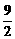 (a2+a26)=
(a2+a26)=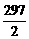 .
.
18.设等差数列{an}共有3n项,它的前2n项和为100,后2n项和是200,则该数列的中间n项和等于 75 .
17.一个等差数列的前12项的和为354,前12项中,偶数项和与奇数项和之比为32∶27,则公差d等于__5 _.
16.等差数列{an}中,若a3+a5=a7-a3=24,则a2=___0___.
15.已知等差数列{an}的公差d =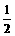 ,且前100项和S100 = 145,那么a1 + a3
+ a5 +…+a99
= 60 .
,且前100项和S100 = 145,那么a1 + a3
+ a5 +…+a99
= 60 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com