13．某校有学生2000人，其中高三学生500人．为了解学生的身体素质情况，采用按年级分层抽样的方法，从该校学生中抽取一个200人的样本，则样本中高三学生的人数为________．

解析：分层抽样即是按比例抽样，易知抽样比例为10?1，故500名高三学生应抽取的人数为50人．

答案：50

12．将容量为100的样本数据，按由小到大排列分成8个组如下表：

第三组的频率和累积频率分别为

(　)

A．0.14和0.37　 　　　　　　　　　　　　　　 B.和

C．0.03和0.06　 　　　　　　　　　　　　　　 D.和

解析：＝0.14，＝＝0.37.

答案：A

11．某地区共有10万户居民，该地区城市住户与农村住户之比为4∶6，根据分层抽样方法，调查了该地区1000户居民拥有冰箱情况，调查结果如下表所示，那么可以估计该地区农村住户中无冰箱的总户数约为

(　)

A.1.6万户　 B．4.4万户

C．1.76万户　 D．0.24万户

解析：根据题目条件可知，本地农村住户共6万户，无冰箱的概率为＝，所以该地区农村住户中无冰箱的总户数约为6×＝＝1.6 万户．

答案：A

10．期中考试以后，班长算出了全班40个同学数学成绩的平均分为M，如果把M当成一个同学的分数，与原来的40个分数一起，算出这41个分数的平均值为N，那么M∶N为

(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　 B．1

C.　 　　　　　　　　　　　　　　　　　　　　　　　 D．2

解析：设40位同学的成绩为x_i(i＝1,2，…，40)，

则M＝，

N＝＝＝M.

故M∶N＝1.

答案：B

9．甲、乙两名射手各打5发子弹，命中环数如下：

甲：6　8　9　9　8

乙：10　7　7　7　9

则两人的射击成绩

(　)

A．甲比乙稳定　 　　　　　　　　　　　　　　 B．乙比甲稳定

C．甲、乙稳定程度相同　 　　　　　　　 D．无法比较

解析：由样本平均数和样本方差的计算公式可得_甲＝_乙，s＜s.

答案：A

8．已知一组数据的方差为m，如果将这组数据中的每个数都乘以2，所得到的一组新数据的方差为

(　)

A．4m　 　　　　　　　　　　　　　　　　　　　　　　　　 B．2m

C．m　 　　　　　　　　　　　　　　　　　　　　　　 D.

解析：设这组数据为x₁，x₂，…，x_n，则

m＝[(x₁－)²+(x₂－)²+…+(x_n－)²]，

而新数据的平均数

′＝(2x₁+2x₂+…+2x_n)＝2，

s′²＝[(2x₁－2)²+(2x₂－2)²+…+(2x_n－2)²]

＝4·[(x₁－)²+(x₂－)²+…+(x_n－)²]

＝4m.

答案：A

7．已知正数a₁，a₂，a₃，a₄，a₅的平均数是x²，将这些数据都减去x后得到的新数据的平均数是6，则x的值是

(　)

A．2　 　　　　　　　　　　　　　　　　　　　　　　 B．3

C．4　 　　　　　　　　　　　　　　　　　　　　　　 D.

解析：∵x²＝，

6＝

＝x²－x，∴x＝－2(舍)或x＝3.

答案：B

6．若数据x₁，x₂，…，x_n的平均数为，方差为s²，则3x₁+5,3x₂+5，…，3x_n+5的平均数和方差分别是

(　)

A.，s²　 　　　　　　　　　　　　　　　　　　　 B．3+5,9s²

C．3+5，s²　 　　　　　　　　　　　　　　　 D．3+5,9s²+30s+25

解析：代入公式易得为B.

答案：B

5．已知样本容量为30，在样本频率分布直方图1中，各小长方形的高比为AE∶BF∶CG∶DH＝2∶4∶3∶1，则第2组的频率和频数分别为

(　)

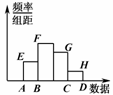
图1

A．0.4,12　 　　　　　　　　　　　　　　　　　　　 B．0.6,16

C．0.4,16　 　　　　　　　　　　　　　　　　　　　 D．0.6,12

解析：频数n₂＝30×＝12，频率f＝＝0.4.

答案：A

4．在样本的频率分布直方图中，一共有m(m≥3)个小矩形，第3个小矩形的面积等于其余m－1个小矩形面积和的，且样本容量为100，则第3组的频数是

(　)

A．0.2　 　　　　　　　　　　　　　　　　　　　　　　　　 B．25

C．20　 　　　　　　　　　　　　　　　　　　　　　 D．以上都不正确

解析：第3组的频率是，样本容量为100，故第3组的频数是100×＝20.选C.

答案：C