练习册

  • 练习册
  • 试题

    题目列表(包括答案和解析)

     0  55781  55789  55795  55799  55805  55807  55811  55817  55819  55825  55831  55835  55837  55841  55847  55849  55855  55859  55861  55865  55867  55871  55873  55875  55876  55877  55879  55880  55881  55883  55885  55889  55891  55895  55897  55901  55907  55909  55915  55919  55921  55925  55931  55937  55939  55945  55949  55951  55957  55961  55967  55975  447348 

    1．已知等差数列{an}满足a2+a4＝4，a3+a5＝10，则它的前10项的和S10＝

    (　)

    A．138　　　　　　　　 B．135

    C．95　 　　　　　　　　　　　　　　 D．23

    解析：由a2+a4＝4，a3+a5＝10可得d＝3，a1＝－4，所以S10＝－4×10+×3＝95.

    答案：C

    试题详情

    22．(14分)有一个容量为100的某校毕业生起始月薪(单位：百元)的样本，数据的分组及各组的频数如下：

    起始月薪
    		 [13,14)
    		 [14,15)
    		 [15,16)
    		 [16,17)
    		 [17,18)
    		 [18,19)
    		 [19,20)
    		 [20,21]
    频数
    		 7
    		 11
    		 26
    		 23
    		 15
    		 8
    		 4
    		 6

    (1)列出样本的频率分布表；

    (2)画出频率分布直方图；

    (3)如果该校毕业生为2000人，试估计该校毕业生起始月薪低于2000元的人数；

    (4)估计该校毕业生起始月薪的平均水平．

    解：(1)样本的频率分布表为

    起始月薪(百元)
    		 频数
    		 频率
    [13,14)
    		 7
    		 0.07
    [14,15)
    		 11
    		 0.11
    [15,16)
    		 26
    		 0.26
    [16,17)
    		 23
    		 0.23
    [17,18)
    		 15
    		 0.15
    [18,19)
    		 8
    		 0.08
    [19,20)
    		 4
    		 0.04
    [20,21)
    		 6
    		 0.06
    合计
    		 100
    		 1.00

    (2)频率分布直方图如图4：

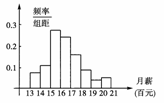
    图4

    (3)起始月薪低于2000元频率为1－0.06＝0.94.

    故起始月薪低于2000元的人数大约是

    2000×0.94＝1880(人)．

    (4)＝×(13.5×7+14.5×11+…+20.5×6)

    ＝16.48(百元)

    所以起始月薪平均水平约为1648元．

    试题详情

    21．(12分)灯泡厂从某日生产的一批灯炮中抽取10个进行寿命测试，得灯泡寿命数据(天)如下：

    30　35　25　25　30　34　26　25　29　21

    求该灯泡的平均寿命估计值和平均方差值S2.

    解：＝＝＝28，

    S2＝[(30－28)2+(35－28)2+(25－28)2+(25－28)2+(30－28)2+(34－28)2+(26－28)2+(25－28)2+(29－28)2+(21－28)2]

    ＝

    ＝＝17.4.

    试题详情

    20．(12分)为了检测某种产品的质量，抽取了一个容量为40的样本，检测结果为一等品8件，二等品18件，三等品12件，次品2件．

    (1)列出样本的频率分布表；

    (2)画出表示样本频率分布的条形图；

    (3)根据上述结果，估计此种新产品为二等品或三等品的概率是多少？

    解：(1)样本的频率分布表为

    样本
    		 频数
    		 频率
    一等品
    		 8
    		 0.2
    二等品
    		 18
    		 0.45
    三等品
    		 12
    		 0.3
    次品
    		 2
    		 0.05

    (2)样本频率分布的条形图如图3：

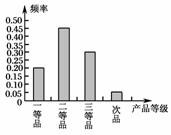
    图3

    (3)根据频率分布表，该产品二等品或三等品的频率为0.45+0.3＝0.75.

    根据上述结果可以估计，此种新产品为二等品或三等品的概率为0.75.

    试题详情

    19．(12分)已知一个样本：25,21,23,25,27,29,25,28,30,29,26,24,25,27,26,22,24,25,26,28.以2为组距，列出频率分布表，并绘出频率分布直方图，并估计样本值出现在22-28之间的概率．

    解：可知最大值为30，最小值为21，组距为2，所以可分5组．频率分布表如下：

    分组
    		 个数累计
    		 频数
    		 频率
    [20.5,22.5)
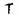    		2
    		 0.10
    [22.5,24.5)
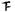    		3
    		 0.15
    [24.5,26.5)
    		 正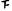
    		 8
    		 0.40
    [26.5,28.5)
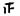    		4
    		 0.20
    [28.5,30.5)
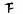    		3
    		 0.15

    频率分布直方图如图2：

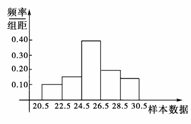
    图2

    样本值出现在22-28之间的概率为0.75.

    试题详情

    18．(12分)某班有50名学生(男生30名，女生20名)，现调查平均身高，准备抽取，问应如何抽样？如果已知男、女生身高有显著差异，又应如何抽样？

    解：(1)运用简单随机抽样方差从50名学生中抽取5名学生作为样本．

    (2)若男、女生身高有显著差异，则运用分层抽样法抽样，分别运用简单随机抽样法从30名男生中抽取3名，从20名女生中抽取2名，将这5名学生组成样本即为所求．

    试题详情

    17．(12分)一个城市有210家商店，其中大型商店有20家，中型商店有40家，小型商店有150家，为掌握各商店的营业情况，要从中抽取一个容量为21的样本，按照分层抽样法抽取样本时，各类商店要抽多少家？写出抽样过程．

    解：抽样比为＝，20×＝2,40×＝4,150×＝15，

    ∴大、中、小型商店各抽2家、4家、15家．

    抽样过程：从20家大型商店中随机抽2家，从40家中型商店中随机抽4家，从150家小型商店中随机抽15家，将此21家商店综合在一起即为样本．

    试题详情

    16．从甲、乙两个总体中各抽取了一个样本：

    甲：900,920,900,850,910,920；

    乙：890,960,950,850,860,890.

    总体波动较小的是________．

    解析：甲＝(0+20+0－50+10+20)+900＝900，

    乙＝(－10+60+50－50－40－10)+900＝900；

    s＝[(900－900)2+(920－900)2+…+(920－900)2]＝≈567，

    s＝[(890－900)2+(960－900)2+…+(890－900)2]＝≈1733.

    ∴波动较小的是甲．

    答案：甲

    试题详情

    15．在样本的频率分布直方图中，共有4个小长方形，这4个小长方形的面积由小到大构成等比数列{an}，已知a2＝2a1，且样本容量为300，则小长方形面积最大的那一组的频数为__________．

    解析：由题可知，4个小长方形的面积分别为a1,2a1,4a1,8a1，且a1+2a1+4a1+8a1＝1，则a1＝，故面积最大的那一组的频数为×300＝160.

    答案：160

    试题详情

    14．利用简单随机抽样法，从n个个体(n＞13)中抽取13个个体，若第二次抽取时，余下的每个个体被抽取到的概率为，则在整个抽样过程中，各个个体被抽取到的概率为________．

    解析：第二次抽取时，余下的每个个体被抽到的概率为，所以余下的人数为36人．所以n＝37.则在整个抽样过程中，各个个体被抽取到的概率为.

    答案：

    试题详情


    同步练习册答案