9．若定义在R上的函数f(x)满足f(+x)＝－f(x)，且f(－x)＝f(x)，则f(x)可以是(　)

A．f(x)＝2sinx　 　　　　　　　 B．f(x)＝2sin3x

C．f(x)＝2cosx　 　　　　　　　 D．f(x)＝2cos3x

解析：∵f(－x)＝f(x)，∴f(x)为偶函数，∴排除A、B.

又∵f(+x)＝－f(x)，∴f(x)是周期为π的函数，

∴选D.

答案：D

8．(2009·江西高考)若函数f(x)＝(1+tanx)cosx,0≤x<，则f(x)的最大值为

(　)

A．1　 　　　　　　　　　　　　　　　 B．2

C.+1　 　　　　　　　　　　　　　 D.+2

解析：f(x)＝(1+·)cosx＝cosx+sinx

＝2(cosx+sinx)＝2sin(x+)．

∵0≤x<，∴≤x+≤.

∴≤sin(x+)≤1.∴1≤f(x)≤2.

答案：B

7．已知函数y＝sin(ωx+φ)(ω>0,0<φ≤)，且此函数的图象如图1所示，由点P(ω，φ)的坐标是

(　)

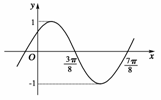
图1

A．(2，)　　　　　　　　　　　 B．(2，)

C．(4，)　　　　　　　　　　　 D．(4，)

解析：由图象可得函数的周期T＝2×(－)＝π＝，得ω＝2，将(，0)代入y＝sin(2x+φ)可得sin(+φ)＝0，由0<φ≤可得φ＝，

∴点(ω，φ)的坐标是(2，)，故选B.

答案：B

6．若α∈[π，π]，则+的值为

(　)

A．2cos　 　　　　　　　　　　　　 B．－2cos

C．2sin　 　　 　　　　　　　　　　 D．－2sin

解析：原式＝+

＝|sin+cos|+|sin－cos|.

∵α∈[，]，∴∈[，]，

当∈[，]时，sin≤cos≤0，

原式＝－(sin+cos)－(sin－cos)

＝－2sin，

当∈[，]时，sin<0，cos≥0.

且|sin|≥|cos|，

∴原式＝－(sin+cos)－(sin－cos)

＝－2sin.

综上，原式＝－2sin.

答案：D

5．将函数f(x)的图象沿x轴向右平移个单位，再将横坐标伸长为原来的2倍(纵坐标不变)，得到的图象所对应的函数为y＝cosx，则f(x)为

(　)

A．y＝cos(2x+)　 　　　　　　 B．y＝cos(2x－)

C．y＝cos(2x+π)　 　　　　　 D．y＝cos(2x－π)

解析：y＝cosxy＝cos2x

y＝cos2(x+)．

答案：C

4．已知2sin²α－sinαcosα+5cos²α＝3，则tanα的值是

(　)

A．1　 　　　　　　　　　　　　　　　 B．－2

C．1或－2　 　　　　　　　　　　　 D．－1或2

解析：由2sin²α－sinαcosα+5cos²α＝3，得

sin²α+sinαcosα－2cos²α＝0，

即tan²α+tanα－2＝0，

解之得tanα＝1或tanα＝－2.

答案：C

3．已知sinαcosα＝，且<α<，则cosα－sinα的值是

(　)

A.　 　　　　　　　　　　　　　　　　 B．－

C．－　 　　　　　　　　　　　　　　 D．±

解析：∵α∈(，)，

∴sinα>cosα，即cosα－sinα<0，

∵(cosα－sinα)²＝1－2sinαcosα＝，

∴cosα－sinα＝－.

答案：B

2．若△ABC的内角满足sinA+cosA>0，tanA－sinA<0，则角A的取值范围是(　)

A．(0，)　 　　　　　　　　　　　 B．(，)

C．(，)　 　　　　　　　　　　　 D．(，π)

解析：由tanA<sinA可知A为钝角，又sinA+cosA>0，结合单位圆可知A∈(，)．

答案：C

1．角α的终边经过点P(x，－)(x≠0)，且cosα＝x，则sinα等于

(　)

A.x　　　　　 B.

C.x　 　　　　　　　　　　　　　　 D．－

解析：r＝，

∵cosα＝x，∴＝，

∴＝，

∴sinα＝＝－＝－.

答案：D

22．(14分)(2009·陕西高考)(理)已知数列{x_n}满足x₁＝，x_n+1＝，n∈N^*.

(1)猜想数列{x_2n}的单调性，并证明你的结论；

(2)证明：|x_n+1－x_n|≤()^n－1.

(文)已知数列{a_n}满足a₁＝1，a₂＝2，a_n+2＝，n∈N^*.

(1)令b_n＝a_n+1－a_n，证明：{b_n}是等比数列；

(2)求{a_n}的通项公式．

解：(理)(1)由x₁＝及x_n+1＝

得x₂＝，x₄＝，x₆＝.

由x₂>x₄>x₆猜想，数列{x_2n}是递减数列．

下面用数学归纳法证明：

①当n＝1时，已证命题成立．

②假设当n＝k时命题成立，即x_2k>x_2k+2，

易知x_n>0，那么x_2k+2－x_2k+4＝－＝＝>0，即x_2(k+1)>x_2(k+1)+2，

也就是说，当n＝k+1时命题也成立．结合①和②知，命题成立．

(2)当n＝1时，|x_n+1－x_n|＝|x₂－x₁|＝，结论成立；

当n≥2时，易知0<x_n－1<1，

∴1+x_n－1<2，x_n＝>，

∴(1+x_n)(1+x_n－1)＝(1+)(1+x_n－1)

＝2+x_n－1≥，

∴|x_n+1－x_n|＝|－|＝≤|x_n－x_n－1|≤()²|x_n－1－x_n－2|≤…≤()^n－1|x₂－x₁|＝()^n－1.

(文)(1)b₁＝a₂－a₁＝1，当n≥2时，b_n＝a_n+1－a_n＝－a_n＝－(a_n－a_n－1)＝－b_n－1，

∴{b_n}是以1为首项，－为公比的等比数列．

(2)由(1)知b_n＝a_n+1－a_n＝(－)^n－1，

当n≥2时，a_n＝a₁+(a₂－a₁)+(a₃－a₂)+…+(a_n－a_n－1)＝1+1+(－)+…+(－)^n－2

＝1+＝1+[1－(－)^n－1]＝－(－)^n－1，当n＝1时，－(－)^1－1＝1＝a₁.

∴a_n＝－(－)^n－1(n∈N^*)．