7．用数字0,1,2,3,4,5可以组成没有重复数字，并且比20000大的五位偶数共有

(　)

A．288个　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．240个

C．144个　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．126个

解析：个位是0的有C·A＝96个；

个位是2的有C·A＝72个；

个位是4的有C·A＝72个；

所以共有96+72+72＝240个．

答案：B

6．(2010·河南郑州质量预测)在(x²－)ⁿ的展开式中含有常数项，则正整数n的最小值是

(　)

A．4　 　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　 B．5

C．6　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．7

解析：其通项为T_r+1＝Cx^2(n－r)(－1)^rx^－3r＝(－1)^rCx^2n－5r.

∵(x²－)ⁿ的展开式中含有常数项，

∴2n－5r＝0，则n的最小值为5，选B.

答案：B

5．用0,1,2，…，9这十个数字组成无重复数字的三位数的个数是

(　)

A．9A　 　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．A

C．A－A　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．A

解析：百位上有9种排法；其他数位上有A种排法．共有9A个三位数，故选A.如用间接法，应为A－A.

答案：A

4．某小组共有8名同学，其中男生6人，女生2人，现从中按性别分层随机抽取4人参加一项公益活动，则不同的抽取方法有

(　)

A．40种　 　　　　　　　　　　　　　　　　　　　　　　　　　　 B．70种

C．80种　 　　　　　　　　　　　　　　　　　　　　　　　　　　 D．240种

解析：依题意得，所选出的4人必是3名男生、1名女生，因此满足题意的抽取方法共有CC＝40种，选A.

答案：A

3．五个人排成一排，甲、乙不相邻，且甲、丙也不相邻的不同排法的种数为

(　)

A．60　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．48

C．36　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．24

解析：五个人排成一排，其中甲、乙不相邻且甲、丙也不相邻的排法可分为两类：一类是甲、乙、丙互不相邻，此类方法有A·A＝12种(先把除甲、乙、丙外的两个人排好，有A种方法，再把甲、乙、丙插入其中，有A种方法，因此此类方法有A·A＝12种)；另一类是乙、丙相邻但不与甲相邻，此类方法有A·A·A＝24种方法(先把除甲、乙、丙外的两人排好，有A种方法，再从这两人所形成的三个空位中任选2个，作为甲和乙、丙的位置，此类方法有A·A·A＝24种)．综上所述，满足题意的方法种数共有12+24＝36，选C.

答案：C

2．(x+2)⁶的展开式中x³的系数为

(　)

A．20　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．40

C．80　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．160

解析：注意到(x+2)⁶的展开式的通项是T_r+1＝C·x^6－r·2^r＝C·2^r·x^6－r，令6－r＝3得r＝3.因此(x+2)⁶的展开式中x³的系数是C·2³＝160，选D.

答案：D

1．(2010·海淀期末)5个人分4张同样的足球票，每人至多分1张，而且票必须分完，那么不同的分法种数是

(　)

A．5⁴　　　　　　　　　　　　　　　　　　　 B．4⁵

C．5×4×3×2　 　　　　　　　　　　　　　　　　　　　　　 D.

解析：依题意得，不同的分法即是从5个人中选出4人来分，因此相应的方法数为C＝，选D.

答案：D

22．(14分)已知函数f(x)＝Asin(ωx+φ)+B(A>0,0<ω<2，|φ|<)的一系列对应值如下表：

(1)根据表格提供的数据求函数y＝f(x)的解析式；

(2)若对任意的实数a，函数y＝f(kx)(k>0)，x∈

(a，a+]的图象与直线y＝1有且仅有两个不同的交点，又当x∈[0，]时，方程f(kx)＝m恰有两个不同的解，求实数m的取值范围．

解：(1)依题意，T＝＝2[－(－)]，∴ω＝1.

又，解得

f()＝2sin(+φ)+1＝3，|φ|<，解得φ＝－

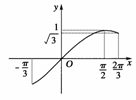
图3

∴f(x)＝2sin(x－)+1为所求．

(2)由已知条件可知，函数y＝f(kx)＝2sin(kx－)+1的周期为，又k>0，∴k＝3

令t＝3x－，∵x∈[0，]，

∴t＝3x－∈[－，]

而y＝sint在[－，]上单调递增，在[，]上单调递减，且sin＝sin＝(如图3)，

∴sint＝s在[－，]上有两个不同的解的充要条件是s∈[，1)，

方程f(x)＝m恰有两个不同的解的充要条件是m∈

[+1,3)．

21．(12分)(2009·江西九校联考)已知函数f(x)＝m·n，其中m＝(sinωx+cosωx，cosωx)，n＝(cosωx－sinωx,2sinωx)，其中ω>0，若f(x)相邻两对称轴间的距离不小于.

(1)求ω的取值范围；

(2)在△ABC中，a，b，c分别是角A，B，C的对边，a＝，b+c＝3，当ω最大时，f(A)＝1，求△ABC的面积．

解：(1)f(x)＝cos²ωx－sin²ωx+2sinωxcosωx＝cos2ωx+sin2ωx＝2sin(2ωx+)．

∵ω>0，∴函数f(x)的周期T＝＝，

由题意可知≥，即T≥π，

解得0<ω≤1，即ω的取值范围是{ω|0<ω≤1}．

(2)由(1)可知ω的最大值为1，

∴f(x)＝2sin(2x+)，

∵f(A)＝1，∴sin(2A+)＝.

而<2A+<π，

∴2A+＝π，∴A＝.

由余弦定理知cosA＝，

∴b²+c²－bc＝3，又b+c＝3，

联立解得或，

∴S_△ABC＝bcsinA＝.

20．(12分)(2009·江苏南京模拟)已知函数f(x)＝2cos²x+

2sinxcosx.

(1)求函数f(x)在[－，]上的值域；

(2)在△ABC中，若f(C)＝2,2sinB＝cos(A－C)－cos(A+C)，求tanA的值．

解：(1)f(x)＝2cos²x+2sinxcosx＝1+cos2x+sin2x

＝2sin(2x+)+1，

∵－≤x≤，

∴－≤2x+≤，－≤sin(2x+)≤1.

∴0≤2sin(2x+)+1≤3.

∴f(x)在区间[－，]上的值域为[0,3]．

(2)f(C)＝2sin(2C+)+1＝2，sin(2C+)＝，

∵0<C<π，∴<2C+<2π+.

∴2C+＝，即C＝.

∵2sinB＝cos(A－C)－cos(A+C)＝2sinAsinC，

∴sin(A+C)＝sinAsinC，sinAcosC+cosAsinC＝sinAsinC，

tanA＝＝＝.