15．(2009·衡阳联考)对于两个非空集合M、P，定义运算：M⊗P＝{x|x∈M，x∈P，且x∉M∩P}．已知集合A＝{x|x²－3x+2＝0}，B＝{y|y＝x²－2x+3，x∈A}，则A⊗B＝__________.

解析：依题意易得A＝{1,2}，B＝{2,3}，A⊗B＝{1,3}．

答案：{1,3}

14．已知集合A＝{x|x²+x－6＝0}，B＝{x|mx+1＝0}，若B⊆A，则m的值为__________．

解析：由题意知，A＝{x|x²+x－6＝0}＝{－3,2}，

因为B⊆A，所以若mx+1＝0有解，则解为－3或2，

当x＝－3时，m＝；

当x＝2时，m＝－.

若mx+1＝0无解，则m＝0.

故m的值为或－或0.

答案：或－或0

13．设集合U＝{1,2,3,4,5}，A＝{2,4}，B＝{3,4,5}，C＝{3,4}，则(A∪B)∩(∁_UC)＝__________.

解析：A∪B＝{2,3,4,5}，∁_UC＝{1,2,5}，故(A∪B)∩∁_UC＝{2,5}．

答案：{2,5}

12．(2009·成都二诊)已知全集U，集合A、B为U的非空真子集，若“x∈A”与“x∈B”是一对互斥事件，则称A与B为一组U(A，B)．规定：U(A，B)≠U(B，A)．当集合U＝{1,2,3,4,5}时，所有的U(A，B)的组数是(　)

A．70　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．30

C．180　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．150

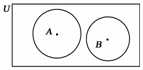
图2

解析：用韦恩图，5个元素填入中间三部分，扣掉A，B为空集，如图2，U(A，B)＝3⁵－2·2⁵+1＝180.

答案：C

11．(2009·长望浏宁模拟)设数集M＝，N＝，且M、N都是集合{x|0≤x≤1}的子集，如果把b－a叫做集合{x|a≤x≤b}的“长度”，那么集合M∩N的“长度”的最小值是　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　 (　)

A. 　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　 B.

C.　　　 　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：M∩N的“长度”最小值为+－1＝，故选D.

答案：D

10．(2009·衡阳联考)已知命题p：函数y＝log_a(ax+2a)(a>0且a≠1)的图象必过定点(－1,1)；命题q：函数y＝

f(x+1)的图象关于原点对称，则y＝f(x)的图象关于点

(－1,0)对称．则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．“p且q”为真　 　　　　　　　　　　　　　　　　　　　 B．“p或q”为假

C．p假q真　 　　　　　　　　　　　　　　　　　　　　　　　　 D．p真q假

解析：命题p为真命题，命题q中f(x)的图象关于点(1,0)对称，∴q为假命题．

答案：D

9．(2010·湖北八校联考)设p：|4x－3|≤1；q：x²－(2a+1)x+a(a+1)≤0.若綈p是綈q的必要而不充分条件，则实数a的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．[0，]　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．(0，)

C．(－∞，0]∪[，+∞) 　 　　　　　　　　　　　　　 D．(－∞，0)∪(，+∞)

解析：∵p：|4x－3|≤1，∴p：≤x≤1，綈p：x>1或x<；∵q：x²－(2a+1)x+a(a+1)≤0，∴q：a≤x≤a+1，綈q：x>a+1或x<a.

又∵綈p是綈q的必要而不充分条件，即綈q⇒綈p，而綈p⇒/ 綈q，∴⇒0≤a≤.故选A.

答案：A

8．有下列四个命题：①{Ø}是空集；②若a∈N，则－a∈N；③集合A＝{x|x∈R|x²－2x+1＝0}有两个元素；④集合B＝{x∈Q|∈N}是有限集，其中正确命题的个数是　　 (　)

A．0　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．1

C．2　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．3

答案：A

7．(2010·唐山一模)已知a>1，g(x)＝a^x2+2x，则g(x)<1成立的一个充分不必要条件是(　)

A．0<x<1　 　　　　　　　　　　　　　　　　　　　　　　　　　　 B．－1<x<0

C．－2<x<0　 　　　　　　　　　　　　　　　　　　　　　　　　 D．－2<x<1

解析：由g(x)<1，得：a^x2+2x<1，又∵a>1　∴x²+2x<0　∴－2<x<0，∵－1<x<0⇒－2<x<0，故选B.

答案：B

6．若命题甲：A∪B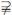A为假命题，命题乙：A∩B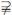A也为假命题，U为全集，则下列四个用文氏图形反映集合A与B的关系中可能正确的是(　)

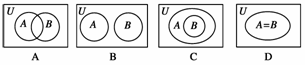
解析：由命题甲：A∪B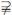A为假命题可知A∪B＝A，由命题乙：A∩B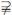A为假命题可知A∩B＝A，所以A＝B，故选D.

答案：D