11．(2010·石家庄质检二)在平面区域D中任取一点，记事件“该点落在其内部一个区域d内”为事件A，则事件A发生的概率P(A)＝.在区间[－1,1]上任取两值a、b，方程x²+ax+b＝0有实数根的概率为P，则

(　)

A．0<P<　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.<P<

C.<P<　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.<P<1

解析：由题意，a、b组成的平面区域是由x＝±1，y＝±1组成的正方形，其面积为4，要保证方程x²+ax+b＝0有实数根，则有Δ＝a²－4b≥0，建立平面直角坐标系如图2，则a²－4b≥0表示的区域即为图中阴影部分，其面积的取值范围是(2，)

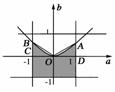
图2

　(其中小三角形AOD和BOC的面积和为××2＝)，∴由题目中的新定义知所求的概率P＝∈(，)，故选B.

答案：B

10．(2009·杭州质检)甲、乙两同学下棋，赢一局得2分，和一局得1分，输一局得1分．连下3局，得分多者为胜．则甲取胜的概率是

(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：下三局，每局都有赢、和、输三种可能，共有3³＝27种，甲取胜分三类：①胜一局，和二局有3种，②胜二局，另一局输和均可，有6种，③胜三局，有1种．故甲取胜概率为，选C.

答案：C

9．(2010·皖南八校联考)某校A班有学生40名，其中男生24人，B班有学生50名，其中女生30人，现从A、B两班各找一名学生进行问卷调查，则找出的学生是一男一女的概率为

(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：所找学生为A班男生B班女生的概率为×，或为B班男生A班女生的概率为×.故所求概率为，选B.

答案：B

8．将一枚硬币连掷5次，如果出现k次正面的概率等于出现k+1次正面的概率，那么k的值为

(　)

A．0　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．1

C．2　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．3

解析：由C()^k()^5－k＝C()^k+1()^5－k－1

即C＝C，

∴k+(k+1)＝5，k＝2.

答案：C

7．某庄园的灌溉系统如图1所示，水从A点入口，进入水流的通道网络，自上而下，从最下面的五个出水口出水，某漂浮物从A点出发向下漂流，在通道交叉口向左下方和向右下方漂流是等可能的，则该漂流物从出口3出来的概率是

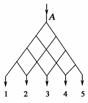
图1

　(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：漂浮物从出口3出来共需漂流4段，其中斜向左下方2段，斜向右下方2段，故共有C种不同漂流路径，而漂浮物从各个出口出来的总路径数为2⁴，故所求概率为＝.

答案：C

6．甲、乙两乒乓球队各有运动员三男两女，其中甲队一男与乙队一女是种子选手，现在两队进行混合双打比赛，则两个种子选手都上场的概率是

(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：甲队种子选手上场的概率为，乙队种子选手上场的概率为.

∴两个种子选手都上场的概率为×＝.

答案：A

5．一个学生通过某英语听力测试的概率是，他连续测试三次，其中恰好有一次通过的概率是　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　

(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：连续测试三次，可看成3次独立重复试验，其中恰有一次通过的概率为P＝C·()·(1－)²＝.

答案：D

4．在100张奖券中，有4张有奖，从这100张奖券中任意抽取2张，2张都中奖的概率是

(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：从总体100张奖券中任取2张的方法有4950种，从4张有奖奖券中抽取2张的方法有6种，故P＝＝.

答案：C

3．甲、乙、丙三人射击命中目标的概率分别为、、，现在三人同时射击一个目标，目标被击中的概率是

(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：1－(1－)(1－)(1－)＝.

答案：C

2．一个均匀的正方体玩具的各个面上分别标以数1,2,3,4,5,6(俗称骰子)，将这个玩具向上抛掷一次，设事件A表示向上的一面出现奇数点(指向上一面的点数是奇数)，事件B表示向上的一面出现的点数不超过3，事件C表示向上的一面出现的点数不少于4，则

(　)

A．A与B是互斥而非对立事件

B．A与B是对立事件

C．B与C是互斥而非对立事件

D．B与C是对立事件

解析：因为事件B与事件C不同时发生且一定有一个发生，所以B与C是对立事件，故选D.

答案：D