9．两圆相交于两点(1,3)和(m,1)，两圆的圆心都在直线x－y+＝0上，则m+c的值是

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．－1 　　　　　　　　　　　　　　　　　 B．2

C．3　 　　　　　　　　　　　　　　　　　　　 D．0

解析：由题意知两点(1,3)、(m,1)的中点(，2)在直线x－y+＝0上，即－2+＝0.∴m+c＝3.

答案：C

8．把直线x－2y+λ＝0向左平移1个单位，再向下平移2个单位后，所得直线正好与圆x²+y²+2x－4y＝0相切，则实数λ的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．3或13　 　　　　　　　　　　　　　　 B．－3或13

C．3或－13　 　　　　　　　　　　　　　 D．－3或－13

解析：直线x－2y+λ＝0按a＝(－1，－2)平移后的直线为x－2y+λ－3＝0，与圆相切，易得λ＝13或3.

答案：A

7．已知有向线段的起点P(－1,1)，终点Q(2,2)，若直线l：x+my+m＝0与有向线段的延长线相交，且过定点

M(0，－1)．如图1，则m的取值范围是　　　　　　　　　　　　　　　　　　 　　　　　　　　　　 (　)

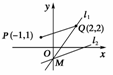
图1

A．(，)

B．(－3，－)

C．(－∞，－3)

D．(－，+∞)

解析：易知k_PQ＝＝，

直线x+my+m＝0过点M(0，－1)．

当m＝0时，直线化为x＝0，一定与PQ相交，所以m≠0，

当m≠0时，k₁＝－，考虑直线l的两个极限位置．

(1)l经过Q，即直线l₁，则kl₁＝＝；

(2)l与平行，即直线l₂，则kl₂＝k_PQ＝，

所以<－<，

即－3<m<－.故选B.

答案：B

6．不等式(x－2y+1)(x+y－3)≤0在坐标平面内表示的区域(用阴影部分表示)，应是下列图形中的　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

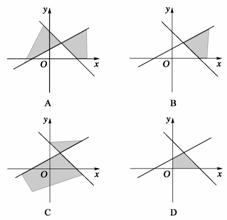
解析：(x－2y+1)(x+y－3)≤0⇔或

答案：C

5．过点(1,3)作直线l，若l过点(a,0)与(0，b)，且a，b∈N^*，则可作出的直线l的条数为　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　 (　)

A．1条 　　　　　　　 　　　　　　　　　　　　　 B．2条

C．3条　 　　　　　　　　　　　　　　　　　 D．多于3条

解析：因为+＝1，且a，b∈N^*，

所以或.故选B.

答案：B

4．直线(a+1)x－y+1－2a＝0与直线(a²－1)x+(a－1)y－15＝0平行，则实数a的值为

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．1　 　　　　　　　　　　　　　　　　　　　 B．－1,1

C．－1　 　　　　　　　　　　　　　　　　　 D．0

解析：将－1,1,0分别代入两直线方程检验得a＝－1符合题意．

答案：C

3．已知两直线x+ay+1＝0与ax－y－3＝0垂直，则a的取值的集合是　　　　　 (　)

A．{－1,1}　　　　　　　　 B．{x|x≠0}

C．R　 　　　　　　　　　　　　　　　　　　 D．Ø

解析：当a＝0时，两直线为x＝－1或y＝－3，则两直线垂直，当a≠0时，两直线的斜率分别为－和a，又－×a＝

－1，则两直线垂直，故a的取值的集合是R，选C.

答案：C

2．若点P(x₀，y₀)在直线Ax+By+C＝0上，则直线方程可表示为　　　　　　　　　　 (　)

A．A(x－x₀)+B(y－y₀)＝0

B．A(x－x₀)－B(y－y₀)＝0

C．B(x－x₀)+A(y－y₀)＝0

D．B(x－x₀)－A(y－y₀)＝0

解析：依题意得Ax₀+By₀+C＝0，即C＝－Ax₀－By₀，代入直线方程得Ax+By－Ax₀－By₀＝0，故直线方程为A(x－x₀)+B(y－y₀)＝0，选A.

答案：A

1．若a+b＝0，则直线y＝ax+b的图象可能是　　　　　　　　　　　　　　　　　　　　　　　 (　)

解析：由a+b＝0得a＝－b，直线在x轴上的截距为－＝1，故选D.

答案：D

22．(14分)(2010·北京东城模拟)甲、乙、丙三人进行某项比赛，每局有两人参加，没有平局，在一局比赛中，甲胜乙的概率为，甲胜丙的概率为，乙胜丙的概率为，比赛的规则是先由甲和乙进行第一局的比赛，然后每局的获胜者与未参加此局比赛的人进行下一局的比赛，在比赛中，有人获胜两局就算取得比赛的胜利，比赛结束．

(1)求只进行两局比赛，甲就取得胜利的概率；

(2)求只进行两局比赛，比赛就结束的概率；

(3)求甲取得比赛胜利的概率．

解：(1)只进行两局比赛，甲就取得胜利的概率为：

P₁＝×＝.

(2)只进行两局比赛，比赛就结束的概率为：

P₂＝×+×＝.

(3)甲取得比赛胜利共有三种情形：

若甲胜乙，甲胜丙，则概率为×＝；

若甲胜乙，甲负丙，丙负乙，甲胜乙，则概率为

×××＝；

若甲负乙，乙负丙，甲胜丙，甲胜乙，则概率为

×××＝.

所以，甲获胜的概率为++＝.